DEFINITION 1. A coloring of a simple graph
is the assignment of a color to each
vertex of the graph so that no two adjacent vertices are
assigned the same color.
DEFINITION 2. The chromatic number of a graph
is the least number of colors needed for a coloring of this graph.
THEOREM1 TheFour ColorTheorem The chromatic number of a
planar graph is no greater than four.
EXAMPLE l What are the chromatic numbers of the graphs G and H shown
in Figure 3 ?

G H

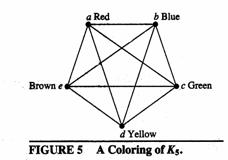
EXAMPLE 2 What is the chromatic number of Kn
?
Solution: A
coloring of Kn can be constructed using n colors by
assigning a different color to each vertex. Is there a coloring using fewer
colors? The answer is no. No two vertices can be assigned the same color, since
every two vertices of this graph are ad- jacent. Hence, the chromatic number of
Kn = n.
(Recall that Kn is not planar
when n ![]() 5, so this
result does not contradict the four color theorem.)
5, so this
result does not contradict the four color theorem.)
A coloring of K5 using five colors is shown
in Figure 5. .
EXAMPLE 3 What is the chromatic number of the
complete bipartite graph K m,n, where m and n are positive integers?
Solution: The
number of colors needed may seem to depend on m and n. However,
only two colors are needed. Color the set of m vertices with one color
and the set of n vertices with a second color. Since edges connect only
a vertex from the set of m vertices and a vertex from the set of n vertices,
no two adjacent vertices have the same color. A coloring of K3,4 with
two colors is displayed in Figure 6. .

EXAMPLE 4 What is the chromatic number of the
graph Cn ? (Recall that Cn is the cycle
with n vertices.)
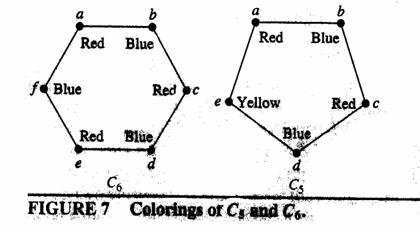
Solution: We
will first consider some individual cases. To begin, let n = 6. Pick a
vertex and color it red. Proceed clockwise in the planar depiction of C6
shown in Figure 7. It is necessary to assign a second color, say blue, to the
next vertex reached.
Continue in the clockwise direction; the third vertex can be
colored red, the fourth vertex blue, and the fifth vertex red. Finally, the
sixth vertex, which is adjacent to the first, can be colored blue. Hence, the
chromatic number of C6 is 2. Figure 7 displays the coloring constructed here.
Next, let n = 5 and consider C5. Pick
a vertex and color it red. Proceeding clock- wise, it is necessary to assign a
second color, say blue, to the next vertex reached.
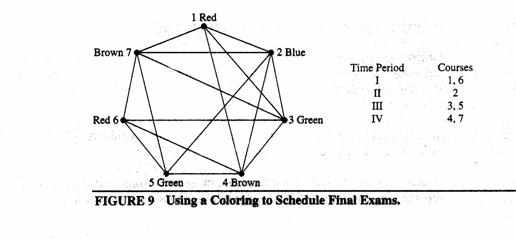
EXAMPLE 5 Scheduling Final Exams How
can the final exams at a university be scheduled so that no student has two
exams at the same time?
Solution: This scheduling problem can be solved using a
graph model, with vertices representing courses and with an edge between two
vertices if there is a common student in the courses they represent. Each time
slot for a final exam is represented by a different color. A scheduling of the
exams corresponds to a coloring of the associated graph.
For instance, suppose there are seven finals to be
scheduled. Suppose the courses are numbered 1 through 7. Suppose that the following
pairs of courses have common students:
1 and 2, 1 and 3, 1 and 4, 1 and 7, 2 and 3, 2 and 4, 2 and 5,
2 and 7, 3 and 4, 3 and 6,3 and7, 4 and 5,4 and 6,5 and 6,
5 and 7, and 6 and7. In Figure 8 the graph associated with
this set of classes is shown. A scheduling consists of a coloring of this
graph. Since the chromatic number of this graph is 4 (the reader should verify
this), four time slots are needed. A coloring of the graph using four colors
and the associated schedule are shown in Figure 9. .