|
|
|
ทฤษฎีบท 2 connected multigraph มีทางเดินออยเลอร์ แต่ไม่ใช่วงจรออยเลอร์ ถ้ามันมีจุด 2 จุด ที่มีดีกรีคี่
ตัวอย่างที่ 4
 |
........กราฟที่แสดงในภาพ 7 มีทางเดินออยเลอร์หรือไม่ |  |
|
|
G1 มีจุด 2 จุด ที่มีดีกรีคี่ คือ b และ d แสดงว่า G1 มีทางเดินออยเลอร์และมี b และ d เป็นจุดสิ้นสุด ตัวอย่างทางเดินออยเลอร์ คือ d , d , b , c , d , b . |
|
G2 มีจุด 2 จุดที่มีดีกรีคี่ คือ b และ f G2 มีทางเดินออยเลอร์และมี b และ f เป็นจุดสิ้นสุด ตัวอย่างทางเดินออยเลอร์คือ b , a , g , f , e , d , c , g , b , c , f . |
||
G3 ไม่มีทางเดินออยเลอร์ เพราะ มีจุดยอด b จุด ทีมีดีกรีคี่ |
||
 |
 |
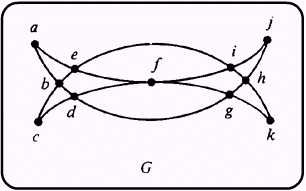
G
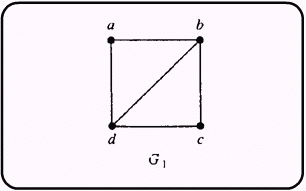
G 1
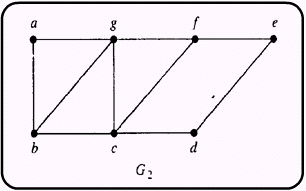
G 2
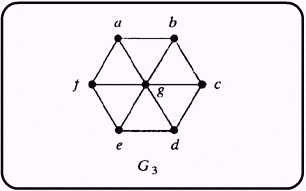
G 3
............ย้อนกลับไปศตวรรษที่ 18 konigsberg มันเป็นไปได้ที่จะเริ่มต้นที่จุดใดจุดหนึ่งในเมืองเดินทางข้ามสะพานทุกสะพาน และสิ้นสุดที่จุดอื่นในเมือง เป็นคำถามที่สามารถหาคำตอบได้โดยการตรวจสอบว่ามีทางเดินออยเลอร์ใน multiograph ที่แสดงสะพาน ใน konigesberg เพราะจุด 4 จุด ใน multigraph มีดีกรีคี่ นั่นคือ ไม่มีทางเดินออยเลอร์ ดังนั้นมันจึงเป็นไปไม่ได้ เงื่อนไขที่จำเป็นและเพียงพอสำหรับทางเดินออยเลอร์และวงจรใน directed graphic (กราฟที่มีทิศทาง) จะพิจารณาในแบบฝึกหัดส่วนท้าย
...............ทางเดินและวงจรของฮาบิลตัน ( Hamiton ) เราได้พัฒนาเงื่อนไขที่จำเป็นและเพียงพอต่อการแสดงว่า มีทางเดิน (path) และวงจร (cirunit) อยู่ ในทุกด้านของ multigraph
..................