
เราสามารถ แทน นิพจน์ซับซ้อน (complicated expressions) เช่น ประพจน์เชิงประกอบ (compound propositions) การจัดหมู่ของเซต (combination of set) และ นิพจน์คำนวณ (arithmetic expressions) โดยใช้ ต้นไม้รากแบบอันดับ ตัวอย่างเช่น จงพิจารณาการแทนที่ ของนิพจน์คำนวณเกี่ยว กับ ตัวปฏิบัติการ +(การบวก), -(การลบ), (การคูณ), /(การหาร), ^(การยกกำลัง) เราจะใช้เครื่องหมาย วงเล็บ เพื่อแสดงถึง ลำดับของ การปฏิบัติการ ต้นไม้รากแบบอันดับ สามารถนำมาใช้ เพื่อแทนนิพจน์ เช่นนี้ได้ เมื่อ จุดภายใน แทน การปฏิบัติการ และ จุดใบ แทน ตัวแปร หรือ ตัวเลข การปฏิบัติการแต่ละชุด กระทำกับ ต้นไม้ส่วนย่อยซ้าย และต้นไม้ส่วนย่อยขวา ตามลำดับ ตัวอย่าง 5 จงวาดรูปต้นไม้รากแบบอันดับ ซึ่งแทนนิพจน์ ((x + y) ^ 2) + ((x - 4) / 3) ผลเฉลย ต้นไม้แบบทวิภาค สำหรับนิพจน์นี้ สามารถสร้างจาก ล่างขึ้นบน (bottom up) ขั้นแรก สร้างต้นไม้ ส่วนย่อย สำหรับ นิพจน์ x + y จากนั้น สิ่งนี้รวมกัน เป็น ต้นไม้ส่วนย่อย ที่มีขนาดใหญ่ขึ้นแทน (x + y) ^ 2 เช่นเดียวกัน สร้างต้นไม้ส่วนย่อย สำหรับ x - 4 และรวมเข้าเป็น ต้นไม้ส่วนย่อย แทน (x - 4)/3 สุดท้าย ต้นไม้ ส่วนย่อย ซึ่งแทน (x + y) ^ 2 และต้นไม้ส่วนย่อยซึ่งแทน (x - 4)/3 รวมเข้าด้วยกัน เป็น ต้นไม้รากแบบอันดับ เพื่อแทน ((x + y) ^ 2) + ((x - 4) / 3) ขั้นตอนเหล่านี้แสดงให้เห็นในรูปที่ 10การแวะผ่านแบบตามลำดับ ของต้นไม้แบบทวิภาค ซึ่งแทนนิพจน์ จะให้นิพจน์เดิม (original expressions) ด้วยสมาชิกและการปฏิบัติการ ในลำดับ เหมือนเช่นเดียวกับ เมื่อมันเกิดตั้งแต่แรก ยกเว้น การดำเนินการ ชนิดเอกภาค (unary operation) ซึ่ง ตัวถูกดำเนินการ (operands) จะตามหลังตัวปฏิบัติ- การทันที ตัวอย่างเช่น การแวะผ่านตามลำดับ ของ ต้นไม้แบบทวิภาค ในรูปที่ 11 ซึ่งแทนนิพจน์ (x + y)/(x + 3), (x + (y/x)) + 3 และ x + (y/(x + 3)) ทั้งสามชุด นี้นำไปสู่ นิพจน์เติมกลาง x + y/x + 3 เพื่อทำ ให้นิพจน์เช่นนี้ ไม่กำกวม (unambiguous) จึงมีความจำเป็นที่จะต้องใส่ เครื่องหมายวงเล็บ ในการแวะผ่าน แบบตามลำดับ เมื่อใดก็ตามที่ พบการปฏิบัติการ นิพจน์ที่มีวงเล็บแบบเต็มรูป ซึ่งได้มาโดยวิธีนี้ เรียกว่า รูปแบบเติมหน้า (infix form) 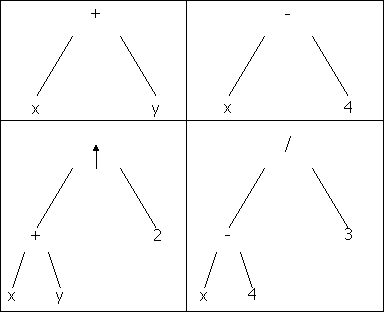
รูปที่ 10 ต้นไม้แบบทวิภาค แทนนิพจน์ ((x+y)^2) = ((x-4)/3)
เราได้ รูปแบบเติมหน้า (infix form) ของนิพจน์ เมื่อเราแวะผ่าน ต้นไม้รากของมัน แบบก่อนลำดับ (preorder) นิพจน์ ซึ่งเขียนด้วย รูปแบบเติมหน้า เรียกว่า สัญกรณ์โพลิช (Polish notation) นิพจน์ ในรูปแบบเติมหน้า (ซึ่งการดำเนินการ แต่ละชุด จะมี ตัวถูกดำเนินการ จำนวน คงที่ ) จะไม่กำกวม ดังนั้น นิพจน์เช่นนี้ จึงไม่จำเป็นต้องมีเครื่องหมายวงเล็บกำกับ ตัวอย่าง 6 จงหารูปแบบเติมหน้า (prefix form) ของนิพจน์ ((x + y) ^ 2) + ((x - 4) / 3) ผลเฉลย เราได้รูปแบบเติมหน้า ของนิพจน์ นี้ โดยการแวะผ่านต้นไม้แบบทวิภาค ซึ่งแทนนิพจน์แสดง ให้เห็น ในรูปที่ 10 ผลลัพธ์คือ + ^ + x y 2 / - x 4 3 ในรูปแบบเติมหน้า ของ นิพจน์ ตัวดำเนินการทวิภาค เช่น + จะอยู่หน้า ตัวถูกดำเนินการ สองตัว ของมัน ดังนั้น เราสามารถประเมินผล นิพจน์ ในรูปแบบเติมหน้า โดย ทำงานจาก ขวาไปซ้าย เมื่อพบตัวดำเนินการ หนึ่งตัว เรากระทำการดำเนินการซึ่งสมนัยกันกับ ตัวถูกดำเนินการสองตัว ทันที ซึ่งอยู่ทางขวา ตัวดำเนินการนี้ เมื่อใดก็ตาม เมื่อการดำเนินการ หนึ่งอย่าง ถูกกระทำ ผลลัพธ์จะเป็นตัว ถูกดำเนินการตัวใหม่ (new operand) ตัวอย่าง 7 จงหาค่าของนิพจน์เติมหน้า + - * 2 3 5 / ^ 2 3 4 ผลเฉลย ขั้นตอนต่างๆ ซึ่งใช้ ประเมินผลนิพจน์ นี้ ทำจาก ขวาไปซ้าย และ กระทำการดำเนินการโดย ใช้ ตัวถูกกระทำ ทางขวา ซึ่งแสดงให้เห็น ในรูปที่ 12 ค่าของนิพจน์นี้ คือ 3
รูปที่ 11 ต้นไม้ราก แทนนิพจน์ (x+y)/(x+y), (x+(x/y))+3, และนิพจน์ x+(y/(x+3))ค่าของนิพจน์ คือ 3 รูปที่ 12 การประเมิณผลนิพจน์เติมหน้า (Evaluating a prefix expression) เราได้ รูปแบบเติมหลัง (postfix form) ของนิพจน์ โดยการ แวะผ่านต้นไม้แบบทวิภาค ของมัน แบบหลังลำดับ นิพจน์ ซึ่ง เขียนด้วย รูปแบบเติมหลัง เรียกว่า สัญกรณ์โพลิชผันกลับ (Reverse Pdolish Notation) นิพจน์ ใน สัญกรณ์โพลิชผันกลับ ไม่กำกวม ดังนั้น จึงไม่จำเป็นต้องใช้เครื่องหมายวงเล็บ ตัวอย่าง 8 จงหารูปแบบเติมหลัง (postfix form) ของนิพจน์ ((x + y) ญ 2) + ((x - 4) / 3) ผลเฉลย รูปแบบเติมหลัง ของนิพจน์ ได้มาโดยการแวะผ่านแบบหลังลำดับ ของต้นไม้แบบทวิภาค สำหรับ นิพจน์นี้ แสดงให้เห็นในรูปที่ 10 ซึ่งให้นิพจน์เติมหลัง ดังนี้ x y + 2 ^ x 4 - 3 / + ในรูปแบบเติมหลัง ของ นิพจน์ ตัวดำเนินการทวิภาค จะตามหลัง (follow) ตัวถูกดำเนินการ สองตัวของมัน ในการประเมินผล นิพจน์ จาก รูปแบบเติมหลัง ทำจากซ้ายไปขวา กระทำ การดำเนินการ เมื่อใดก็ตามที่มี ตัวดำเนินการหนึ่งตัวตามหลกังตัวถูกดำเนินการสองตัว หลังจาก การดำเนินการ หนึ่ง อย่าง ทำสำเร็จแล้ว ผลลัพธ์ของการดำเนินการนี้ จะเป็น ตัวถูกดำเนินการตัวใหม่ (new operand) ตัวอย่าง 9 จงหาค่าของ นิพจน์เติมหลัง 7 2 3 * - 4 ^ 9 3 / + ผลเฉลย ขั้นตอนต่างๆ ซึ่ง ใช้ประเมินผลนิพจน์นี้ เริ่มต้น จากซ้าย และกระทำการดำเนินการให้ได้ผลลัพธ์ เมื่อมี ตัวถูกดำเนินการ สองตัว ตามด้วย ตัวดำเนินการหนึ่งตัว แสดงให้เห็น ในรูปที่ 13 ค่าของนิพจน์นี้ เท่ากับ 4เนื่องจากนิพจน์เติมหน้า และ นิพจน์เติมหลัง ไม่กำกวม และเพราะว่า มันประเมินผลง่าย ไม่ต้องทำการ กราดตรวจ(scanning) กลับไป กลับมา นิพจน์เหล่านี้ จึงถูกรำมาใช้ อย่างกว้างขวาง ใน วิชา คอมพิวเตอร์ นิพจน์เช่นนี้ มีประโยชน์โดยเฉพาะ ในการสร้างคอมไพเลอร์ (compilers) รูปที่ 15 การประเมิณผลนิพจน์เติมหลัง (Evaluating a postfix expression)