
บทนิยาม 4.1 ให้ ![]() และ
และ ![]() เป็นจุด 2 จุดในระนาบ
และให้ k เป็นจำนวนซึ่งมากกว่าระยะทางระหว่าง
เป็นจุด 2 จุดในระนาบ
และให้ k เป็นจำนวนซึ่งมากกว่าระยะทางระหว่าง ![]() และ
และ ![]()
เซตของจุด P ทั้งหมดในระนาบซึ่ง
![]()
เรียกว่าวงรี จุด ![]() และ
และ ![]() เรียกว่าโฟกัสของวงรี
เรียกว่าโฟกัสของวงรี
จุดกึ่งกลางของส่วนของเส้นตรง ระหว่างจุดโฟกัสทั้ง 2 เรียกจุดศูนย์กลางของวงรี
ดังรูปที่ 4.1
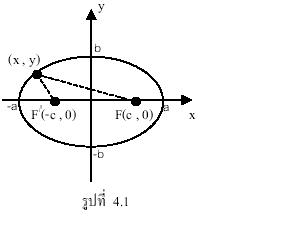
ถ้าให้โฟกัสคือจุด (-c , 0) และ
(c , 0) เมื่อ c > 0
แล้วระยะทางระหว่างโฟกัส คือ 2c
เพื่อความสะดวกเราให้ k = 2a เมื่อ ![]() โดยสมมุติฐาน
2a = k > 2c นั่นคือ a > c
โดยสมมุติฐาน
2a = k > 2c นั่นคือ a > c
ถ้า (x , y) เป็นจุดบนวงรีแล้วจะได้ว่า
![]()
หรือ ![]()
![]()
หรือ ![]()
ยกกำลังสองทั้งสองข้างอีกครั้งหนึ่งจะได้
![]()
หรือ ![]() (4.1)
(4.1)
เพราะว่า ![]() เพราะฉะนั้น
เพราะฉะนั้น ![]()
ให้ ![]() ตรวจสอบได้ว่า
ตรวจสอบได้ว่า ![]()
แทน ![]() ในสมการ (4.1) จะได้
ในสมการ (4.1) จะได้ ![]()
หรือ 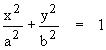 (4.2)
(4.2)
สมการ (4.2) เป็นสมการของวงรีซึ่งมีจุดศูนย์กลางที่จุดกำเนิด
โฟกัสที่จุด
F/(-c , 0) และ F(c , 0)
ตัดแกน x ที่จุด
(a , 0) และ (-a, 0)
ตัดแกน y ที่จุด
(0, b) และ(0, -b)
เรียกจุด (-a
, 0) และ (a , 0) ว่าจุดยอดของวงรี
และ
ส่วนของเส้นตรงที่อยู่ระหว่างจุดยอด
(-a , 0) และ (a , 0) เรียกว่าแกนเอก (major - axis) ของวงรี
และ
ส่วนของเส้นตรงระหว่าง
(0 , -b ) และ (0 ,b) เรียกว่า แกนโท (minor axis) ของวงรี
กราฟของสมการใน 4.2 แสดงได้ดังรูปที่ 4.2
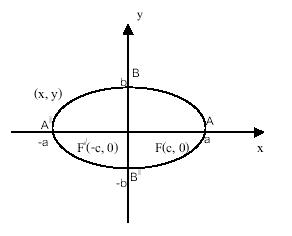
รูปที่ 4.2
เป็นแกนเอก
เป็นแกนโท
ในทำนองเดียวกันถ้าโฟกัสของวงรีอยู่บนแกน
y คือ จุด (0 , c) และ(0, -c) เมื่อ c > 0 แล้วสมการวงรี
อยู่ในรูปมาตรฐานเป็น
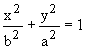 (4.3)
(4.3)
กราฟของสมการใน (4.3) แสดงได้ดังรูปที่ 4.3
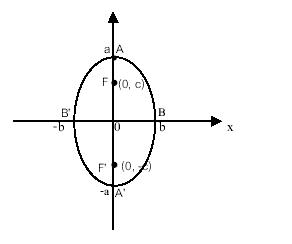
สรุป เราได้สมการของวงรีในรูปมาตรฐาน 2 แบบคือและ
เป็นโฟกัส
และ
เป็นจุดยอด
เป็นแกนเอก
เป็นแกนโท
![]()

![]()

2b = ความยาวของแกนโท
,
2c = ระยะระหว่างโฟกัส
ตัวอย่าง 4.1
จงเขียนกราฟของวรี ที่มีความยาวของแกนเอกเป็น 12 หน่วย และมีโฟกัสอยู่ที่จุด
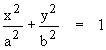
ความยาวของแกนเอกเท่ากับ 2 a ดังนั้น
![]() หรือ
หรือ ![]()
โฟกัสอยู่ที่จุด (-4, 0) และ (4,
0) จะได้ ![]()
เนื่องจาก ![]() จะได้
จะได้
![]()
สมการวงรีคือ
![]()
ดังรูปที่ 4.4
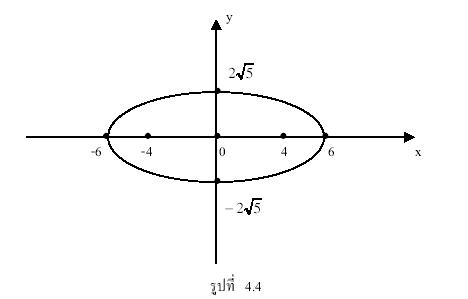
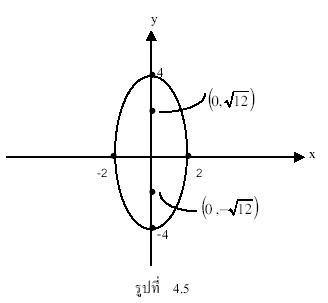
ตัวอย่าง 4.2 จงเขียนกราฟของสมการ ![]()
วิธีทำ เขียนสมการที่กำหนดให้ ในรูป
![]() (4.4)
(4.4)
ดังนั้นกราฟวงรีนี้มีจุดศูนย์กลางที่จุดกำเนิด แกนเอกอยู่บนแกน y จะได้ว่า
![]() และ
และ ![]()
ดังนั้น ![]()
ในการเขียนกราฟจะกำหนดจุด 4 จุด คือ
(-2, 0) , (2, 0) , (0, -4) และ (0, 4)
โดยมีจุดโฟกัสคือจุด ![]() และ
และ ![]()
แสดงได้ดังรูปที่ 4.5
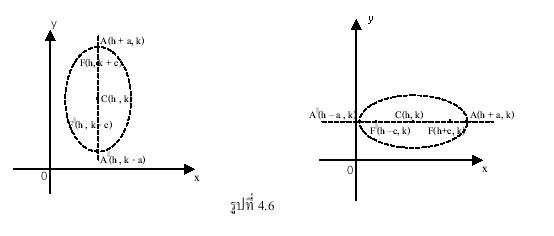
ถ้าจุดศูนย์กลางของวงรีอยู่ที่ ![]()
![]() และแกนเอกขนานกับแกน x หรือขนานกับแกน y
และแกนเอกขนานกับแกน x หรือขนานกับแกน y
การหาสมการของวงรีในกรณีนี้ทำได้โดยเลื่อนแกนพิกัด
x และ y ให้จุดกำเนิด ![]() ไปอยู่ที่จุด
ไปอยู่ที่จุด
![]()
![]() จะได้สมการของวงรีในรูปมาตรฐานเทียบกับแกน
จะได้สมการของวงรีในรูปมาตรฐานเทียบกับแกน ![]() และ
และ ![]() คือ
คือ
![]() หรือ
หรือ ![]() (5.1)
(5.1)
เมื่อ ![]() และ
และ ![]() แทนค่าในสมการ (5.1)
จะได้
แทนค่าในสมการ (5.1)
จะได้
![]() (5.2)
(5.2)
หรือ ![]() (5.3)
(5.3)
ตามลำดับ
โดยการกระจายสมการ (5.2) และสมการ (5.3) และจัดรูปใหม่ได้สมการวงรีแบบทั่วไปคือ
![]() , เมื่อ
, เมื่อ ![]() (5.4)
(5.4)
ตัวอย่าง 4.3
กำหนดสมการ ![]() จงหาจุดโฟกัส จุดยอด พร้อมทั้ง
จงหาจุดโฟกัส จุดยอด พร้อมทั้ง
เขียนกราฟ
วิธีทำ จากสมการที่กำหนดให้ โดยวิธีกำลังสองสัมบูรณ์ของ x และ y
จะได้ ![]()
![]()
หรือ ![]()
ให้ ![]() และ
และ ![]() จะได้
จะได้
![]()
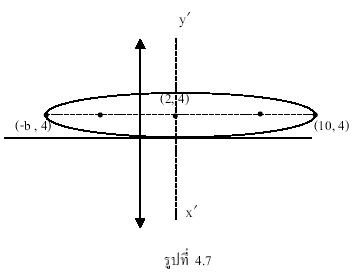
ดังนั้นย้ายจุดกำเนิดไปที่ (2,
4) และแกน ![]() ขนานกับแกนเดิมสมการที่กำหนดให้เป็นสมการวงรี
ขนานกับแกนเดิมสมการที่กำหนดให้เป็นสมการวงรี
จุดศูนย์กลางอยู่ที่ (2, 4) เทียบกับแกนเดิม
เนื่องจาก a = 8 ดังนั้นจุดยอดคือ
![]()
และ ![]()
กราฟของวงรีแสดงได้ดังรูป