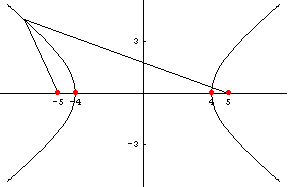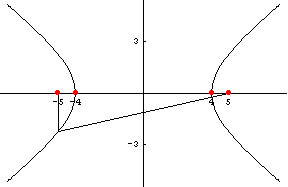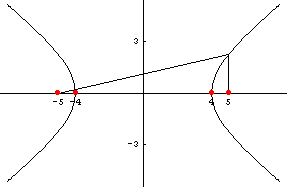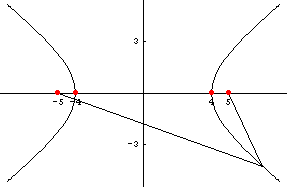

บทนิยาม 5.1 ให้ ![]() และ
และ ![]() เป็นจุด 2 จุด ที่ต่างกันในระนาบ
และให้ k เป็นจำนวนบวกซึ่ง
เป็นจุด 2 จุด ที่ต่างกันในระนาบ
และให้ k เป็นจำนวนบวกซึ่ง
น้อยกว่าระยะทางระหว่าง ![]() และ
และ ![]()
เซตของจุด P ทั้งหมดในระนาบที่
![]()
เรียกว่าไฮเพอร์โบลา จุด ![]() และ
และ![]() เรียกว่าโฟกัสของไฮเพอร์โบลา
เรียกว่าโฟกัสของไฮเพอร์โบลา
จุดกึ่งกลางระหว่างโฟกัสทั้ง 2 เรียกว่าจุด ศูนย์กลางของไฮเพอร์โบลา ดังรูป 5.1

เรากล่าวว่าไฮเพอร์โบลา อยู่ในรูปมาตรฐาน ถ้าจุดศูนย์กลางอยู่ ณ จุดกำเนิด และ โฟกัสอยู่บนแกน x หรือ แกน y
ถ้าให้โฟกัสคือจุด (-c , 0) และ (c , 0) เมื่อ c > 0 (ดังรูปที่ 5.1) แล้วระยะทางระหว่างโฟกัส คือ 2c เพื่อความสะดวก ให้ k = 2a เมื่อ a > 0 โดยสมมติฐาน 2a = k < 2c นั่นคือ a < c
ถ้า (x , y) เป็นจุดบนไฮเพอร์โบลาแล้วจะได้ว่า
![]()
หรือ ![]()
ยกกำลังสองทั้งสองข้างจะได้
![]()
หรือ ![]()
ยกกำลังสองทั้งสองข้างอีกครั้งหนึ่ง จะได้
![]()
หรือ ![]() (5.1)
(5.1)
เพราะว่า ![]() เพราะฉะนั้น
เพราะฉะนั้น ![]()
ให้ ![]()
แทน ![]() ในสมการ (6.1) จะได้
ในสมการ (6.1) จะได้ ![]()
หรือ ![]() (5.2)
(5.2)
สมการ (5.2) เป็นสมการไฮเพอร์โบลา
ซึ่งมีจุดศูนย์กลางที่จุดกำเนิด โฟกัสที่จุด ![]() และ
และ ![]() ตัดแกน x ที่จุด (a
, 0) และ (-a , 0) เรียกว่าจุดยอดของไฮเพอร์โบลา และส่วนของเส้นตรงที่อยู่ระหว่าง
ตัดแกน x ที่จุด (a
, 0) และ (-a , 0) เรียกว่าจุดยอดของไฮเพอร์โบลา และส่วนของเส้นตรงที่อยู่ระหว่าง
จุดยอด (-a , 0) และ (a , 0) เรียกว่า แกนตามขวางของไฮเพอร์โบลา ส่วนของเส้นตรงระหว่างจุด (0, -b)
และ (0 , b) เรียกว่า แกนสังยุคของไฮเพอร์โบลา กราฟของสมการใน (5.2) แสดงได้ดังรูปที่ (5.2)

ในทำนองเดียวกัน ถ้าโฟกัสของไฮเพอร์โบลาอยู่บนแกน
y คือ
จุด (0 , c) และ (0 , -c) เมื่อ
c > 0
แล้วสมการไฮเพอร์โบลา อยู่ในรูปมาตรฐานเป็น
![]() (5.3)
(5.3)
กราฟของสมการใน (5.3) แสดงได้ดังรูปที่ (5.3)

จากสมการ (5.2) เมื่อ y > 0 เราพบว่า
![]()
แสดงว่าไฮเพอร์โบลาเข้าใกล้เส้นตรง ![]() ขณะ x เข้าใกล้
ขณะ x เข้าใกล้ ![]() เพราะว่าไฮเพอร์โบลา
เพราะว่าไฮเพอร์โบลา
สมมาตรเทียบกับแกน x ดังนั้นไฮเพอร์โบลาเข้าใกล้เส้น ![]() เช่นกัน เราเรียกเส้นตรง
เช่นกัน เราเรียกเส้นตรง
![]() และ
และ ![]()
ว่าเส้นกำกับของไฮเพอร์โบลา
ในทำนองเดียวกัน ถ้าไฮเพอร์โบลาสมการเป็นสมการใน (5.3) จะได้ว่า
เส้นกำกับของไฮเพอร์โบลา คือ ![]() และ
และ ![]() ดังรูปที่ 5.4
ดังรูปที่ 5.4

สรุป เราได้สมการของไฮเพอร์โบลาในรูปมาตรฐาน 2 แบบ
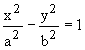

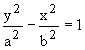
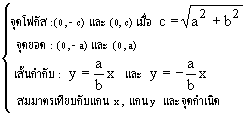
2a = ความยาวแกนตามขวาง
2c = ระยะระหว่างโฟกัสทั้งสอง
ตัวอย่าง 5.1 กำหนดจุด (0, 3) และ (0, -3) เป็นจุดยอดของไฮเพอร์โบลา และโฟกัสที่จุด (0, 5) และ
(0, -5) จงหาสมการของไฮเพอร์โบลา
วิธีทำ เนื่องจากโฟกัสอยู่บนแกน y ดังนั้นแกนตามขวางจะทับกับแกน y จุดศูนย์กลางคือ (0, 0)
สมการไฮเพอร์โบลามีรูปมาตรฐานคือ
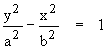
ระยะระหว่างจุดยอด
= ![]()
ระยะระหว่างโฟกัส
= ![]()
ดังนั้น ![]() และ
และ ![]()
เนื่องจาก ![]() จะได้
จะได้ ![]()
ดังนั้น ![]()
สมการไฮเพอร์โบลาคือ ![]()
ตัวอย่าง 5.2
จงเขียนกราฟของสมการ ![]() พร้อมทั้งหาจุดโฟกัส และ ความ
พร้อมทั้งหาจุดโฟกัส และ ความ
ยาวแกนตามขวาง สมการเส้นกำกับ
วิธีทำ เขียนสมการที่กำหนดให้อยู่ในรูป ![]()
ดังนั้น ![]() และ
และ ![]()
กราฟของสมการไฮเพอร์โบลาเป็นกราฟที่มีจุดศูนย์กลางที่จุดกำเนิด และมีแกนตามขวางทับกับแกน x
จุดยอดคือ (3, 0) , (-3, 0)
เนื่องจาก ![]() ดังนั้น
จะได้
ดังนั้น
จะได้
![]() หรือ
หรือ ![]()
ดังนั้น โฟกัสอยู่ที่จุด ![]() และ
และ ![]()
สมการเส้นกำกับคือ ![]() และ
และ ![]()
ความยาวแกนตามขวาง ![]() แสดงได้ดังรูปที่ 5.5
แสดงได้ดังรูปที่ 5.5

ถ้าไฮเพอร์โบลาไม่ได้อยู่ในรูปมาตรฐาน สมมุติจุดศูนย์กลางอยู่ที่ (h , k) และแกนตามขวางขนานแกน x (หรือแกน y) โดยการย้ายแกน จะได้สมการ
 (6.5)
(6.5)
หรือ  (6.6)
(6.6)
กระจาย (6.5) หรือ (6.6) และเขียนใหม่ได้สมการรูปทั่วไป คือ
![]() เมื่อ
เมื่อ ![]() (6.7)
(6.7)
ตัวอย่างที่ 6.3 กำหนดให้สมการ ![]() จงหาจุดยอด และสมการเส้น
จงหาจุดยอด และสมการเส้น
กำกับเทียบกับแกนเดิม
วิธีทำ โดยวิธีกำลังสองสัมบูรณ์ของ x และ y จะได้
![]()
![]()
![]()
![]()
ให้ ![]() และ
และ ![]()
ดังนั้นสมการจะเขียนได้เป็น
![]()
ดังนั้นเลื่อนจุดกำเนิดไปที่จุด (3, 1) และแกนขนานกับแกนเดิม สมการไฮเพอร์โบลาที่กำหนดให้
มีจุดศูนย์กลางที่ (3, 1) เทียบกับแกนเดิม เนื่องจาก a = 3 ดังนั้นจุดยอดคือ (3, 4) และ (3, -2)
สมการเส้นกำกับเทียบกับแกน ![]() คือ
คือ ![]() และ
และ ![]()
ดังนั้นสมการเส้นกำกับเทียบกับแกนเดิมคือ
![]() หรือ
หรือ ![]()
แสดงได้ดังรูปที่ 5.6
