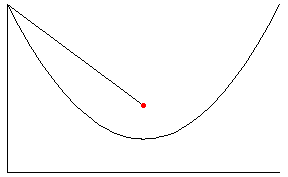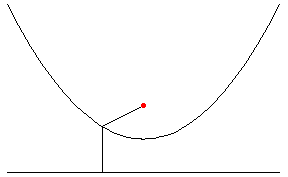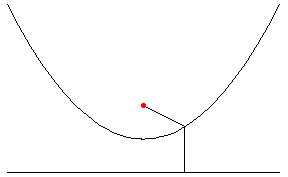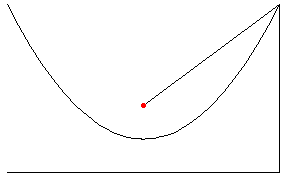
บทนิยาม 1.1 ให้  เป็นเส้นตรงบนระนาบ และ F เป็นจุดบนระนาบที่ไม่ได้อยู่บนเส้นตรง 

เซตของจุดทั้งหมดบนระนาบซึ่งอยู่ห่างจากเส้นตรง  และ F เป็นระยะทางเท่ากัน เรียกว่า พาราโบลา เส้นตรง  เรียกว่า ไดเรกตริกซ์ (directrix) และจุด F เรียกว่า โฟกัส (focus)ของพาราโบลา
เส้นตรงที่ผ่านโฟกัสและตั้งฉากกับไดเรกตริกซ์ เรียกว่า แกนของพาราโบลา
จุดที่อยู่ถึงกลางระหว่างโฟกัสและไดเรกตริกซ์ เรียกว่า จุดยอดของพาราโบลา

ดังรูปที่ 1.5

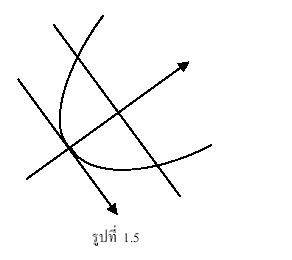
ถ้าจุดยอดอยู่ที่จุดกำเนิด และแกนของพาราโบลา คือแกน x หรือ แกน y เรากล่าวว่า

พาราโบลาอยู่ในรูปมาตรฐาน ดังรูป 1.6

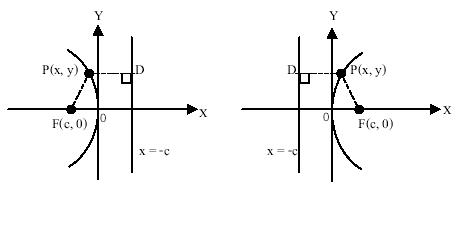
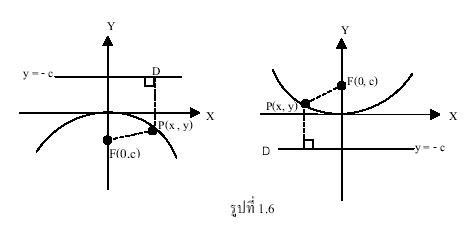
ต่อไปจะหาสมการของพาราโบลารูปมาตรฐาน

       พิจารณาพาราโบลาที่มีโฟกัสอยู่ที่จุด (0, c) เมื่อ  ไดเรกตริกซ์คือเส้นตรง   และแกนของพาราโบลาคือแกน y

ให้  เป็นจุดใดๆ บนพาราโบลา และ PD ตั้งฉากกับไดเรกตริกซ์ที่จุด D

ดังรูปที่ 1.7

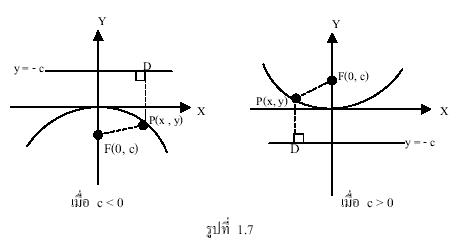
จากบทนิยาม 1.1 จะได้ว่า 

เพราะฉะนั้น 

จัดรูปให้ง่ายได้เป็น

ถ้า c > 0 , เป็นสมการของพาราโบลาที่มีกราฟเปิดข้างบน หรือ กราฟหงายขึ้น

ถ้า  เป็นสมการของพาราโบลาที่มีกราฟเปิดข้างล่าง หรือกราฟคว่ำลง

ในทำนองเดียวกัน ถ้าพาราโบลามีโฟกัสอยู่ที่จุด (c , 0) เมื่อ  ไดเรกตริกซ์คือ

เส้นตรง  และแกนของพาราโบลาคือแกน x

จะได้สมการ

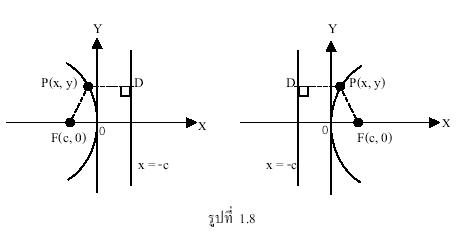
ถ้า  เป็นสมการของพาราโบลาที่มีกราฟเปิดทางขวา

ถ้า  เป็นสมการของพาราโบลาที่มีกราฟเปิดทางซ้าย

สรุป สมการของพาราโบลาในรูปมาตรฐาน

และ

= ระยะทางจากโฟกัสถึงไดเรกตริกซ์

ตัวอย่าง 1.1 จงหาสมการของพาราโบลาที่มีเงื่อนไขดังต่อไปนี้ พร้อมทั้งเขียนกราฟ

1) มีโฟกัสอยู่ที่จุด (-3, 0) และไดเรกตริกซ์เส้นตรง x = 3

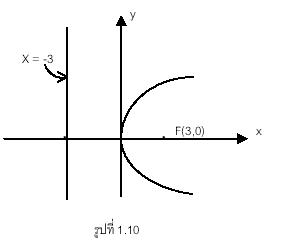
2) มีโฟกัสอยู่ที่จุด (3, 0) และไดเรกตริกซ์เส้นตรง x = -3

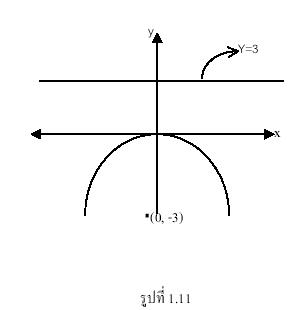
3) มีโฟกัสอยู่ที่จุด (0, -3) และไดเรกตริกซ์เส้นตรง y = 3

4) มีโฟกัสอยู่ที่จุด (0, 3) และไดเรกตริกซ์เส้นตรง y = -3
 
 

วิธีทำ 1) มีโฟกัสอยู่ที่จุด (-3, 0) และไดเรกตริกซ์เส้นตรง x = 3

สมการพาราโบลามีไดเรกตริกซ์คือเส้นตรง x = 3

เพราะฉะนั้น -c = 3 หรือ c = -3

จากรูปสมการมาตรฐานของพาราโบลาที่มีโฟกัสที่จุด (c , 0) และไดเรกตริกซ์คือเส้นตรง

x = -c คือ  แทนค่า c = -3 จะได้สมการพาราโบลา 

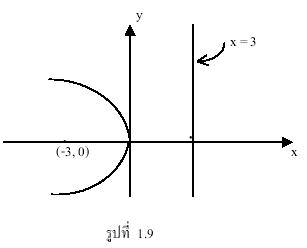
2) มีโฟกัสอยู่ที่จุด (3, 0) และไดเรกตริกซ์เส้นตรง x = -3

สมการพาราโบลามีไดเรกตริกซ์คือเส้นตรง x = -3 เพราะฉะนั้น -c = -3 หรือ c = 3

จากรูปสมการมาตรฐานของพาราโบลาที่มีโฟกัสที่จุด (c , 0) และไดเรกตริกซ์คือเส้นตรง

x = -c คือ  แทนค่า c = -3 จะได้สมการพาราโบลา 

3) มีโฟกัสอยู่ที่จุด (0, -3) และไดเรกตริกซ์เส้นตรง y = 3

สมการพาราโบลามีไดเรกตริกซ์คือเส้นตรง y = 3

เพราะฉะนั้น -c = 3 หรือ c = -3

จากรูปสมการมาตรฐานของพาราโบลาที่มีโฟกัสที่จุด (0, c) และไดเรกตริกซ์คือเส้นตรง

y = -c คือ  แทนค่า c = -3 จะได้สมการพาราโบลา 

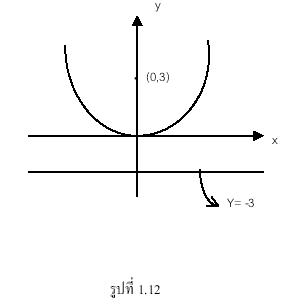
4) มีโฟกัสอยู่ที่จุด (0, 3) และไดเรกตริกซ์เส้นตรง y = -3

สมการพาราโบลามีไดเรกตริกซ์คือเส้นตรง y = -3 เพราะฉะนั้น -c = -3 หรือ c = 3

จากรูปสมการมาตรฐานของพาราโบลาที่มีโฟกัสที่จุด (0, c) และไดเรกตริกซ์คือเส้นตรง

y = -c คือ  แทนค่า c = 3 จะได้สมการพาราโบลา 

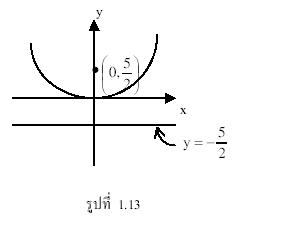
ตัวอย่าง 1.2 จงหาโฟกัส และไดเรกตริกซ์ของพาราโบลา 

วิธีทำ จากสมการพาราโบลาที่กำหนด

เมื่อเทียบกับสมการมาตรฐาน 

จะได้ว่า  หรือ 

ดังนั้นโฟกัสคือจุด  และไดเรกตริกซ์คือเส้นตรง  ดังรูปที่ 1.13

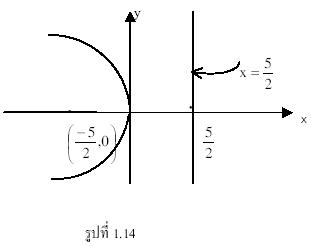
ตัวอย่าง 1.3 จงหาโฟกัส และไดเรกตริกซ์ของพาราโบลา 

วิธีทำ จากสมการพาราโบลาที่กำหนด

เมื่อเทียบกับสมการมาตรฐาน 

จะได้ว่า  หรือ 

ดังนั้นโฟกัสคือจุด  และไดเรกตริกซ์คือเส้นตรง  ดังรูปที่ 1.14