อนุพันธ์ย่อย
ให้ $f(x,y) $ เป็นฟังก์ชัน สองตัวแปร $(a,b) \in D_f $
จะนิยามอนุพันธ์ย่อย ของ $f(x,y) $ ที่จุด $(a,b) $ ดังนี้
- อนุพันธ์ย่อยของ $f(x,y) $ เทียบกับ $x$ ที่จุด $(a,b) $ เขียนแทนด้วย $f_x (a,b) $คือ
$lim_{h \to 0 } \frac{f(a+h,b)-f(a,b)}{h}$ เมื่อลิมิตหาค่าได้
- อนุพันธ์ย่อยของ $f(x,y) $ เทียบกับ $y $ ที่จุด $(a,b) $ เขียนแทนด้วย $f_y (a,b) $ คือ
$lim_{h \to 0 } \frac{f(a,b+h)-f(a,b)}{h}$ เมื่อลิมิตหาค่าได้
ดังนั้น
- อนุพันธ์ย่อยของ $f(x,y) $ เทียบกับ $x$ ที่จุด $(x,y) $ ใด ๆ เขียนแทนด้วย $f_x (x,y) $คือ
$lim_{h \to 0 } \frac{f(x+h,y)-f(x,y)}{h}$ เมื่อลิมิตหาค่าได้
- อนุพันธ์ย่อยของ $f(x,y) $ เทียบกับ $y $ ที่จุด $(x,y) $ เขียนแทนด้วย $f_y (x,y) $ คือ
$lim_{h \to 0 } \frac{f(x,y+h)-f(x,y)}{h}$ เมื่อลิมิตหาค่าได้
นอกจากนี้ อาจใช้สัญลักษณ์สำหรับอนุพันธ์ย่อย ดังนี้
ถ้า $z=f(x,y) $ แล้ว อนุพันธ์ย่อย สามารถเขียนแทนด้วย
- $f_x(x,y) \quad = f_x \quad = \frac{\partial f }{\partial x } \quad = \frac{\partial }{\partial x } f(x,y) \quad = \frac{\partial z }{\partial x } $
- $f_y (x,y) \quad = f_y \quad = \frac{\partial f }{\partial y } \quad = \frac{\partial }{\partial y } f(x,y) \quad = \frac{\partial z }{\partial y } $
ตัวอย่าง
ให้ $f(x,y) = x^2+y^3+ 4xy + 5x+6y +7 $ จงหา
- $f_x (x,y) $ และ $ f_y (x,y) $
- $f_x (0,-1)$ และ $ f_y (0,-1) $
วิธีทำ
ในการหาค่า $f_x (x,y) $ ใช้ วิธีการหาอนุพันธของฟังก์ชัน หนึ่งตัวแปร
โดยการหาอนุพันธ์ ของ $f(x,y)$ เทียบกับ $x$ โดยการมองตัวแปร $y$ เป็นค่าคงตัว
ดังนั้น $f_x (x,y) \quad = 2x+0+4y+5+6(0)+0 \quad = 2x+4y+5 $
จึงได้ว่า $f_x (0,-1) \quad = 2(0)+4(-1)+5 \quad = 1 $
ในทำนองเดียวกัน ในการหาค่า $f_y (x,y) $ ใช้ วิธีการหาอนุพันธของฟังก์ชัน หนึ่งตัวแปร
โดยการหาอนุพันธ์ ของ $f(x,y)$ เทียบกับ $y$ โดยการมองตัวแปร $x$ เป็นค่าคงตัว
ดังนั้น $f_y (x,y) \quad = 0+3y^2+4x+0+6+0 \quad = 3y^2+4x+6 $
จึงได้ว่า $f_y (0,-1) \quad = 3(-1)^2+4(0)+6 \quad = 9 $
ความหมายทางเรขาคณิต
ให้ $z=f(x,y) $ แล้วจะได้ว่า
$f_x (a,b) $ คือ ความชันของเส้นโค้งที่เกิดจากการตัดกันระหว่าง พื้นผิว $z=f(x,y)$ กับระนาบ $y = b $ ที่จุด $( a,b,f(a,b) )$ ดังรูป
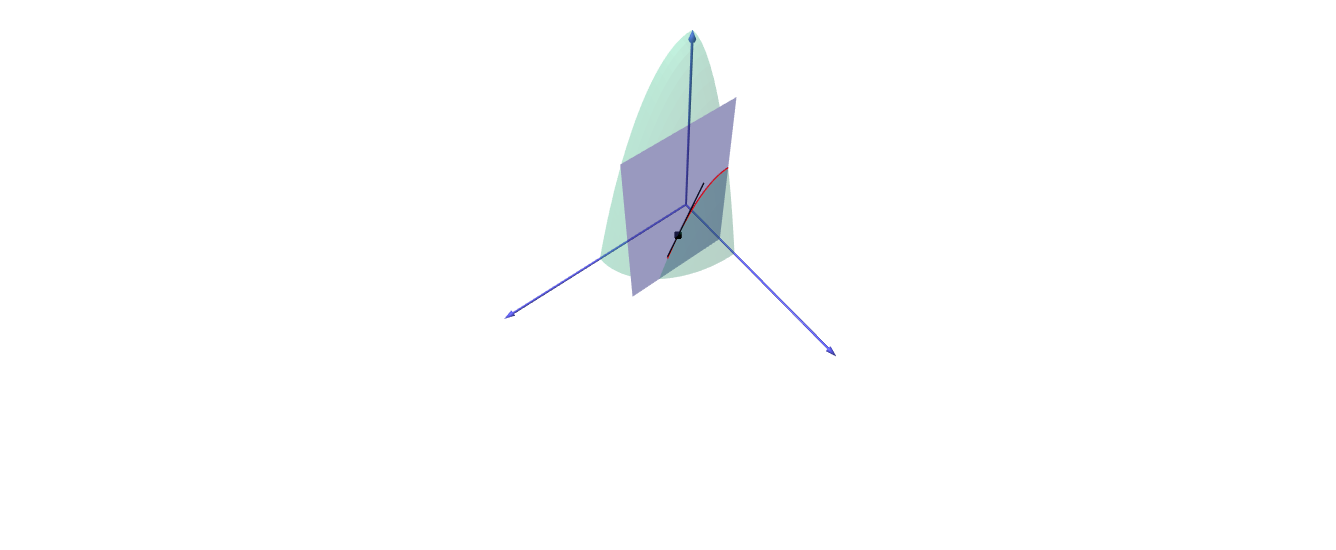
ในทำนองเดียวกัน
$f_y (a,b) $ คือ ความชันของเส้นโค้งที่เกิดจากการตัดกันระหว่าง พื้นผิว $z=f(x,y)$ กับระนาบ $x = a $ ที่จุด $( a,b,f(a,b) )$ ดังรูป
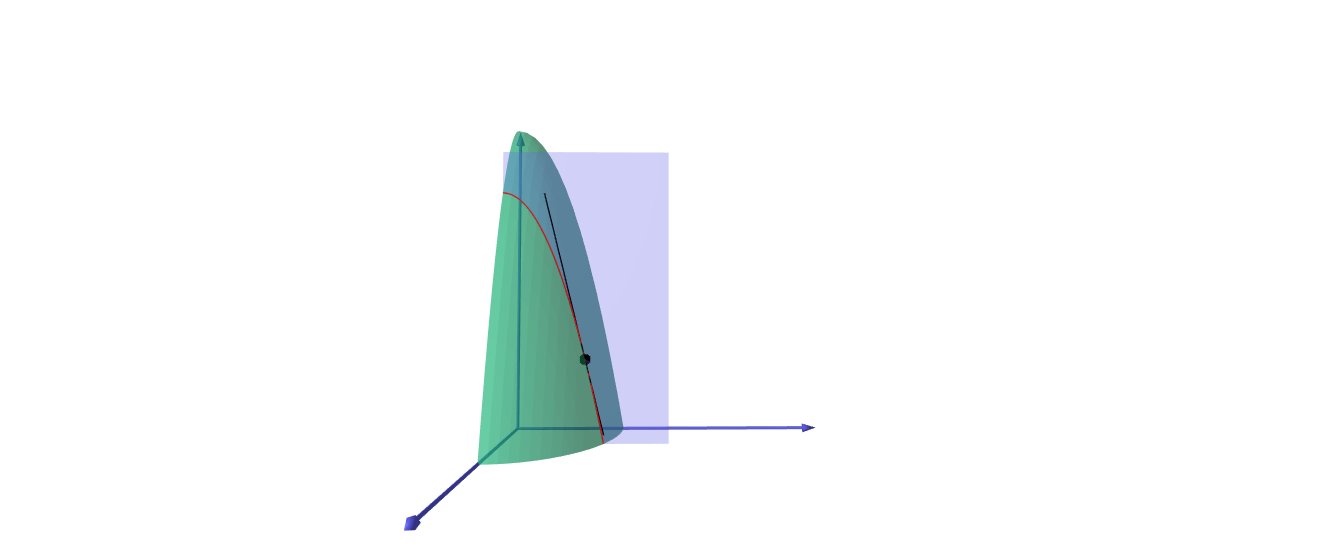
สำหรับฟังก์ชัน สามตัวแปร $w=f(x,y,z) $
สามารถนิยามอนุพันธ์ย่อยในทำนองเดียวกัน
- อนุพันธ์ย่อยของ $f(x,y,z) $ เทียบกับ $x$ ที่จุด $(a,b,c) $ เขียนแทนด้วย $f_x (a,b,c) $คือ
$lim_{h \to 0 } \frac{f(a+h,b,c)-f(a,b,c)}{h}$ เมื่อลิมิตหาค่าได้
- อนุพันธ์ย่อยของ $f(x,y,z) $ เทียบกับ $y$ ที่จุด $(a,b,c) $ เขียนแทนด้วย $f_y (a,b,c) $คือ
$lim_{h \to 0 } \frac{f(a,b+h,c)-f(a,b,c)}{h}$ เมื่อลิมิตหาค่าได้
- อนุพันธ์ย่อยของ $f(x,y,z) $ เทียบกับ $z$ ที่จุด $(a,b,c) $ เขียนแทนด้วย $f_z (a,b,c) $คือ
$lim_{h \to 0 } \frac{f(a,b,c+h)-f(a,b,c)}{h}$ เมื่อลิมิตหาค่าได้
จาก ฟังก์ชัน สอง และ สามตัวแปร สามารถ ขยายออกไปถึง ฟังก์ชัน $n$ ตัวแปรได้ในทำนองเดียวกัน
ตัวอย่าง
จงหา $f_x, \quad f_y, \quad f_z $ เมื่อ
- $f(x,y,z) = x^2 y^3 z^4 + x \sin y \cos z +y e^x + 2z $
- $f(x,y,z) = x \ln y + y \ln z + z \ln x +xyz $
วิธีทำ
- $f_x (x,y,z) = 2x y^3 z^4 + \sin y \cos z +y e^x \\
f_y (x,y,z) = 3 x^2 y^2 z^4 + x \cos y \cos z + e^x \\
f_z (x,y,z) =4 x^2 y^3 z^3 - x \sin y \sin z + 2$
- $f_x (x,y,z) = \ln y + \frac{z}{x} + yz \\
f_y (x,y,z) =\frac{x}{y} + \ln z + xz \\
f_z (x,y,z) = \frac{y}{z} + \ln x +xy $
สามารถใช้โปรแกรม SageMath ดังนี้
อนุพันธ์ย่อยอันดับสูง
ให้ $ z= f(x,y) $ เป็นฟังก์ชันสองตัวแปร
จะเรียกอนุพันธ์ย่อยของ $f_x (x,y) $ ว่าอนุพันธ์ย่อยอันดับ 2 ของ ฟังก์ชัน $f(x,y) $ มีดังนี้
- อนุพันธ์ย่อยของ $f_x (x,y) $ เทียบกับ $x$ เขียนแทนด้วย $f_{xx} (x,y) = \big( f_x (x,y) \big ) _x $
- อนุพันธ์ย่อยของ $f_x (x,y) $ เทียบกับ $y$ เขียนแทนด้วย $f_{xy} (x,y) = \big( f_x (x,y) \big ) _y $
ทำนองเดียวกัน
- อนุพันธ์ย่อยของ $f_y (x,y) $ เทียบกับ $x$ เขียนแทนด้วย $f_{yx} (x,y) = \big( f_y (x,y) \big ) _x $
- อนุพันธ์ย่อยของ $f_y (x,y) $ เทียบกับ $y$ เขียนแทนด้วย $f_{yy} (x,y) = \big( f_y (x,y) \big ) _y $
นอกจากนี้ อาจใช้สัญลักษณ์สำหรับอนุพันธ์ย่อย อันดับ 2 ดังนี้
- $f_{xx} (x,y) \quad = f_{xx} \quad = \frac{\partial ^2 f }{\partial x^2 } \quad = \frac{\partial ^2 }{\partial x^2 } f(x,y) \quad = \frac{\partial ^2 z }{\partial x^2 } $
- $f_{xy} (x,y) \quad = f_{xy} \quad = \frac{\partial ^2 f }{\partial y \partial x } \quad = \frac{\partial ^2 }{\partial y \partial x } f(x,y) \quad = \frac{\partial ^2 z }{\partial y \partial x } $
- $f_{yx} (x,y) \quad = f_{yx} \quad = \frac{\partial ^2 f }{\partial x \partial y } \quad = \frac{\partial ^2 }{\partial x \partial y } f(x,y) \quad = \frac{\partial ^2 z }{\partial x \partial y } $
- $f_{yy} (x,y) \quad = f_{yy} \quad = \frac{\partial ^2 f }{ \partial y^2 } \quad = \frac{\partial ^2 }{\partial y^2 } f(x,y) \quad = \frac{\partial ^2 z }{ \partial y^2 } $
โดยทั่วไป $f_{xy} (a,b) \neq f_{yx}(a,b) $
ดังตัวอย่างต่อไปนี้
ทฤษฎีบท
ให้ $f(x,y)$ เป็นฟังก์ชันที่นิยามและต่อเนื่องบนโดเมน $D$ จุด $(a,b) \in D $
ถ้า $f_{xy} $ และ $f_{yx}$ ทั้งคู่ต่อเนื่องบนโดเมน $D$ แล้ว $$ f_{xy} (a,b) = f_{yx}(a,b) $$
สำหรับอนุพันธ์ย่อย ของฟังก์ชัน $z=f(x,y) $อันดับสูงกว่า 2 ก็จะนิยาม และใช้สัญลักษณ ในทำนองเดียวกัน เช่น
$f_{xyxx}(x,y) $ หมายถึงอนุพันธ์ย่อยอันดับ 4 โดย หาอนุพันธ์ย่อย ของ $f(x,y)$ เทียบกับ $x $ เทียบกับ $y $ เทียบกับ $x $ แล้ว เทียบกับ $x $ ตามลำดับ
และ
$\frac{\partial ^4 z }{ \partial x^2 \partial y^2 } $ หมายถึงอนุพันธ์ย่อยอันดับ 4 โดย หาอนุพันธ์ย่อย ของ $f(x,y)$ เทียบกับ $y $ เทียบกับ $y $ เทียบกับ $x $ แล้ว เทียบกับ $x $ ตามลำดับ
กรณี ฟังก์ชัน มากกว่า สองตัวแปร ก็สามารถ นิยาม และใช้สัญลักษณ์ เหมือนกันกับ สองตัวแปร
เช่น
ให้ $w=f(x,y,z) $ ความหมายของ $f_{xzyz} (x,y,z)$ แทนอนุพันธ์ย่อยอันดับ 4 ของฟังก์ชัน $f(x,y,z)$ โดย หาอนุพันธ์ย่อย ของ $f(x,y,z)$ เทียบกับ $x $ เทียบกับ $z $ เทียบกับ $y $ แล้ว เทียบกับ $z $ ตามลำดับ
ตัวอย่าง
ให้ $f(x,y,z) = y^2 \sin (x+2z)$ จงหา $f_{yzxz} $
วิธีทำ
$$ f_y \quad = 2y \sin (x+2z) \\ f_{yz} \quad = 4y \cos (x+2z) \\
f_{yzx} \quad = -4y \sin (x+2z) \\ f_{yzxz} \quad = -8y \cos (x+2z)$$
สามารถใช้โปรแกรม SageMath ดังนี้

