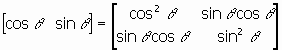A = ![]()
จงหาเมทริกซ์มาตรฐานสำหรับ orthogonal projection P ของ R2 บนเส้น l ที่ผ่านจุดกำเนิด และทำมุม q กับแกน x
วิธีทำ
เส้นตรง l เป็นปริภูมิย่อย 1 มิติของ R2 เราสามารถให้ v = (cos q , sin q ) เป็นฐานหลักของปริภูมิย่อยนี้ ดังนั้น
A = ![]()
สามารถแสดงได้ว่า ATA เป็นเมทริกซ์เอกลักษณ์มิติ 1? 1 จากสูตรที่ 6 จะได้
[P] = AAT =![]()