
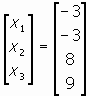
ตัวอย่างที่ 2 Orthogonal Projection on a Subspace
จงหา orthogonal projection ของเวกเตอร์ u = (-3,-3,8,9) บนปริภูมิย่อยของ R4 ที่แผ่ทั่วถึงโดยเวกเตอร์ u1 = (3,1,0,1), u2 = (1,2,1,1), u3 = (-1,0,2,-1)วิธีทำ
เราสามารถแก้ปัญหานี้โดยใช้วิธีการของ Gram - Schmidt ในการเปลี่ยน (u1, u2, u3) เป็น orthogonal basis และประยุกต์วิธีการที่ใช้ในตัวอย่างที่ 6 ของ หัวข้อ 6.3 แต่อย่างไรก็ตามวิธีการต่อไปนี้มีประสิทธิภาพมากกว่าปริภูมิย่อย W ใน R4 ซึ่งแผ่ทั่วถึงโดย u1, u2, และ u3 เป็น column space ของเมทริกซ์
A =
ดังนั้น, ถ้า u ถูกใช้เป็น column vector เราสามารถหา orthogonal projection ของ u บน W โดยหา least square solution ของระบบ Ax = u และคำนวณหา projw u = Ax จาก least square solution การคำนวณทำได้ดังต่อไปนี้, ระบบ Ax = u

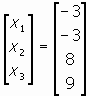
ดังนั้น
ATA =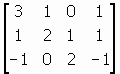
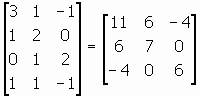 ATu =
ATu = 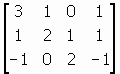
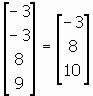
ระบบสมการทั่วไป ATAx = ATu ในกรณีนี้ จะได้
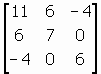
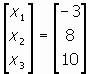
ได้คำตอบของ least square solution ของ Ax = u คือ
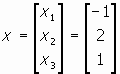
ดังนั้น
projwu = Ax =

หรือเขียนเป็นสัญลักษณ์ที่สอดคล้องกับโจทย์ได้ ดังนี้
projw u = (-2,3,4,0)ในหัวข้อที่ 4.2 เราได้กล่าวถึงตัวดำเนินการพื้นฐานของ orthogonal projection บน R2 และ R3 (ตารางที่ 4 และ 5) โดยความคิดในเรื่องตัวดำเนินการของ orthogonal projection สามารถที่จะขยายไปสู่ปริภูมิแบบยูคลิดที่ขนาดใหญ่ ขึ้นได้ดังนี้
|
Definition |
|
|
ถ้า W เป็นปริภูมิย่อยของ Rm แล้วผลการแปลง P:Rm ® W จะโยงแต่ละเวกเตอร์ x ใน Rm ไปยัง orthogonal projection เรียกว่า orthogonal projection ของ Rm บน W |
|
ซึ่งจะได้ว่า orthogonal projection เป็นการดำเนินการตามเส้น จากสูตรที่ (5) เมทริกซ์พื้นฐานของ orthogonal projection ของ Rm บน W คือ
[P] = A(ATA)-1ATโดยที่ A ถูกสร้างโดยใช้ฐานหลักของ W เป็น column เวกเตอร์