ปริพันธ์จำกัดเขต
บทนิยาม
ให้ฟังก์ชัน $ f(x) $ เป็นฟังก์ชันที่หาค่าได้บนช่วงปิด [a,b]
$ P = \{ a=x_0 < x_1 < ...< x_{n-1} < x_n=b \}$ เป็นเซตของผลแบ่งกั้นบนช่วงปิด [a,b]
เลือก $ x_i^* \in [x_{i-1},x_i] $ เมื่อ $ i = 1,2,...,n$
จะเรียกค่า
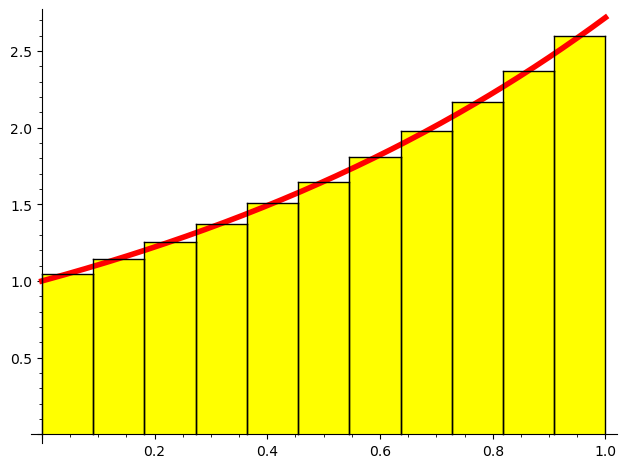
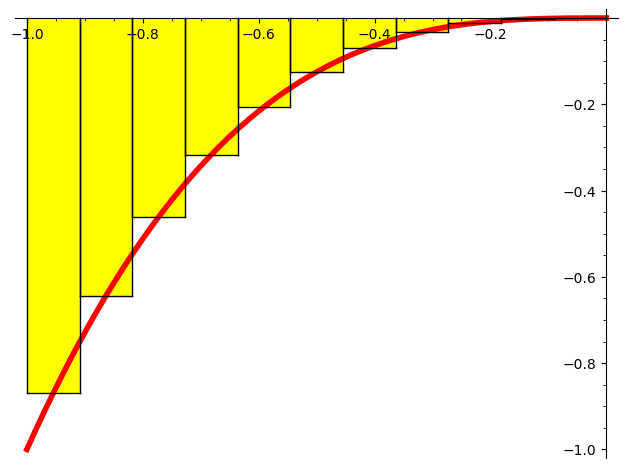
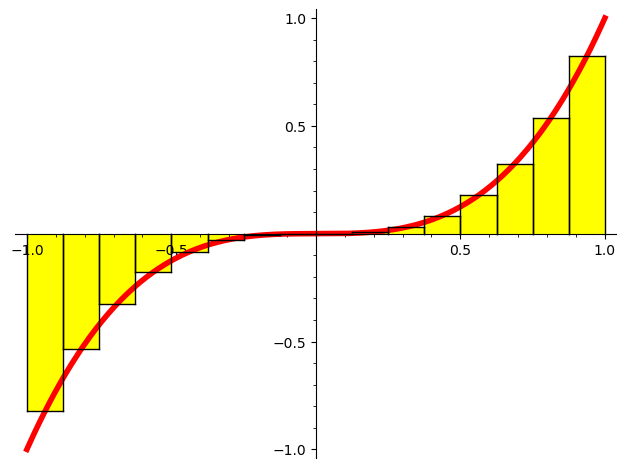
$$ \lim_{n \to \infty } \sum_{i=1}^n f(x_i^*)*(x_i - x_{i-1})$$
ว่าปริพันธ์จำกัดเขต ของ $f$ บนช่วงปิด [a,b] เมื่อ ลิมิตเป็นจำนวนจริง
เขียนแทนด้วย $$\int_a^b f(x) dx$$
ทฤษฎีบท
ถ้า $f$ ต่อเนื่องบนช่วงปิด [a,b] และกำหนด
$$ g(x) = \int_a^x f(t) dt $$ เมื่อ $x \in [a,b] $
แล้ว $ g $ จะต่อเนื่องบนช่วงปิด [a,b] และหาอนุพันธ์ได้บนช่วงเปิด (a,b) และได้ว่า
$$g'(x) = f(x) $$
ทฤษฎีบท
ถ้า $f$ ต่อเนื่องบนช่วงปิด [a,b] ดังนั้น
$$ \int_a^b f(x) dx = F(b) - F(a) $$ เมื่อ $ F $ คือปฎิยานุพันธ์ของ $f$ หรือ $F'(x) = f(x) $
หมายเหต
เขียนแทน $$ F(b)-F(a) = F(x) \Bigg |_a^b $$
สมบัติปริพันธ์จำกัดเขต
$
\begin{align}
& 1. \int_a^b c dx = c(b-a) \\
& 2. \int_a^b (f(x)+g(x) ) dx = \int_a^b f(x) dx + \int_a^b g(x) dx \\
& 3. \int_a^b c f(x) dx =c \int_a^b f(x) dx \\
& 4. \int_a^a f(x) dx =0 \\
& 5. \int_a^b f(x) dx = - \int_b^a f(x) dx \\
& 6. \int_a^t f(x) dx +\int_t^b f(x) dx = \int_a^b f(x) dx \quad เมื่อ t \in [a,b]
\end{align}
$
ตัวอย่าง
จงหาค่าปริพันธ์จำกัดเขต
$
\begin{align}
&1. \int_0^1 x dx & &
2. \int_{-1}^0 x dx \\
&3. \int_{-1}^1 x dx &&
4. \int_0^1 (1-x)^9 dx \\
&5. \int_1^9 \frac{x-1}{\sqrt{x}} dx &&
6. \int_{-1}^2 t(2+t^7) dt \\
& 7. \int_{-\pi/4}^{\pi/4} \sec ^2 t dt &&
8. \int_0^1 (3+u \sqrt{u} )du \\
& 9. \int_{-1}^2 |x| dx &&
10. \int_0^{12} | x - 6 | dx \\
\end{align}
$
สามารถใช้โปรแกรม SageMath ดังนี้


