ปริมาตรที่เกิดจากการหมุนพื้นที่
ให้ $S $ เป็นรูปทรง 3 มิติ ที่อยู่ระหว่าง ระนาบ $x=a$ และระนาบ $x=b$ ถ้าภาคตัดขวางของรูปทรงสามมิติ $S$ ที่เกิดจากระนาบ$P_x$ ที่ตั้งฉากกับแกน$x$ ตัดกับ$S$มีพื้นที่รอยตัดคือ $A(x)$ โดยที่ $A(x)$ เป็นฟังก์ชันที่ต่อเนื่องบนช่วงปิด [a,b]
แล้ว ปริมาตรของ$S$ คือ
$$ V = \int_a^b A(x) dx $$
ตัวอย่าง
จงแสดงว่า ปริมาตรของรูปทรงกลมที่มีรัศมี $r$ คือ $\frac{4}{3} \pi r^3 $
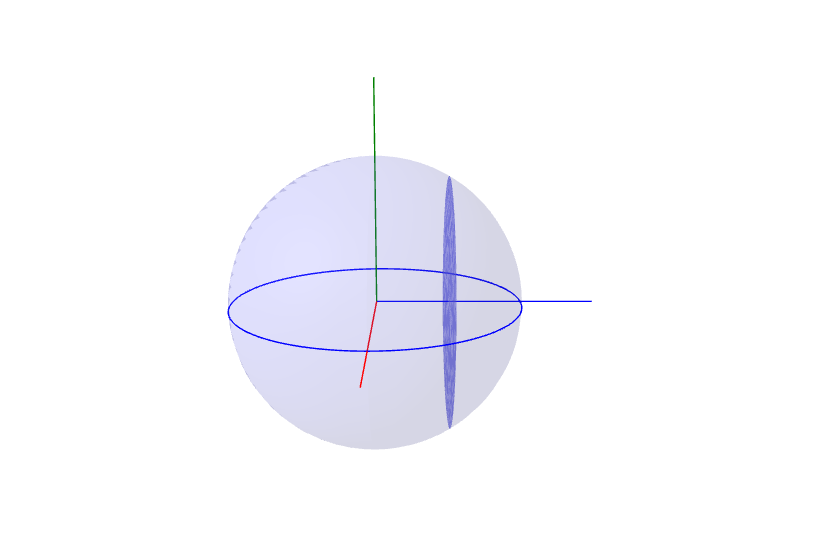
วิธีทำ
เนื่องจากภาคตัดขวางที่ตำแหน่ง $x$ ใดๆ จะเป็นวงกลมที่มีรัศมี $y$ โดยที่ $y=\sqrt{r^2-x^2}$
ดังนั้น พื้นที่ภาคตัดขวางคือ $$ A(x) = \pi y^2 =\pi (r^2-x^2) $$
นั่นคือ ปริมาตรรูปทรงกลมคือ
$$V = \int_{-r}^r A(x) dx \\
= \int_{-r}^r \pi (r^2-x^2) dx\\
= \pi (r^2 x-\frac{x^3}{3} )\Bigg |_{-r}^r \\
= \pi ( (r^3-\frac{r^3}{3}) - (-r^3+\frac{r^3}{3}) )\\
= \frac{4}{3} \pi r^3 $$
สำหรับการหาปริมาตรของรูปทรงสามมิติที่เกิดจากการหมุนพื้นที่ $R $รอบแกนพิกัดแกน (แกน x หรือ แกน y) หรือรอบเส้นตรงที่ขนานกับแกนพิกัด
ซึ่งในที่นี้เราจะพิจารณาวิธีหา 2 วิธี คือ
1. วิธีแบบจาน
2. วิธีแบบเปลือกทรงกระบอก
1. การหาปริมาตรของรูปทรงสามมิติโดยวิธีแบบจาน
ให้ $f$ เป็นฟังก์ชันที่ต่อเนื่องและ$f(x) \geq 0 $ทุก $x$ ในช่วงปิด [ a , b] และ
$R$ เป็นบริเวณที่อยู่ใต้เส้นโค้ง $y=f(x)$ แต่อยู่เหนือแกน $x $ สำหรับ $a \leq x \leq b $
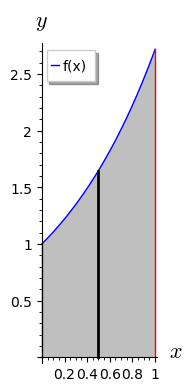
จะได้ว่า ปริมาตรของรูปทรงสามมิติที่เกิดจากการหมุน บริเวณ $R$ รอบแกน $x$ คือ
$$ V = \int_a^b \pi [f(x)]^2 dx $$
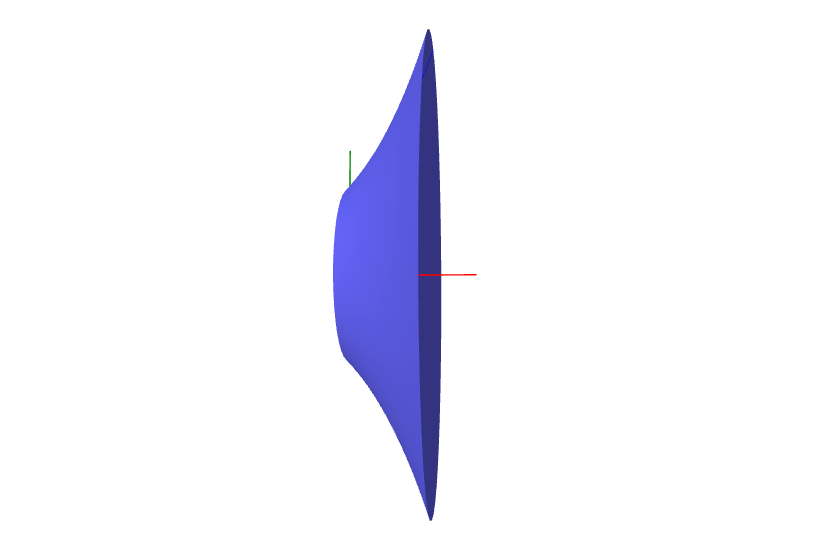

ให้ $f,g $ เป็นฟังก์ชันที่ต่อเนื่องและ$f(x) \geq g(x) \geq 0 $ทุก $x$ ในช่วงปิด [ a , b] และ
$R$ เป็นบริเวณที่อยูระหว่าง เส้นโค้ง $y=f(x),y=g(x) $ สำหรับ $a \leq x \leq b $
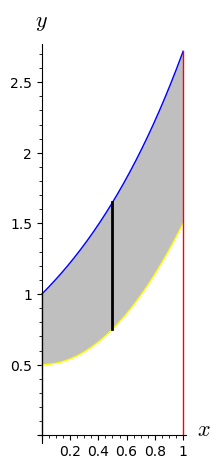
จะได้ว่า ปริมาตรของรูปทรงสามมิติที่เกิดจากการหมุน บริเวณ $R$ รอบแกน $x$ คือ
$$ V = \int_a^b \pi ( [f(x)]^2 - [g(x)]^2 ) dx $$
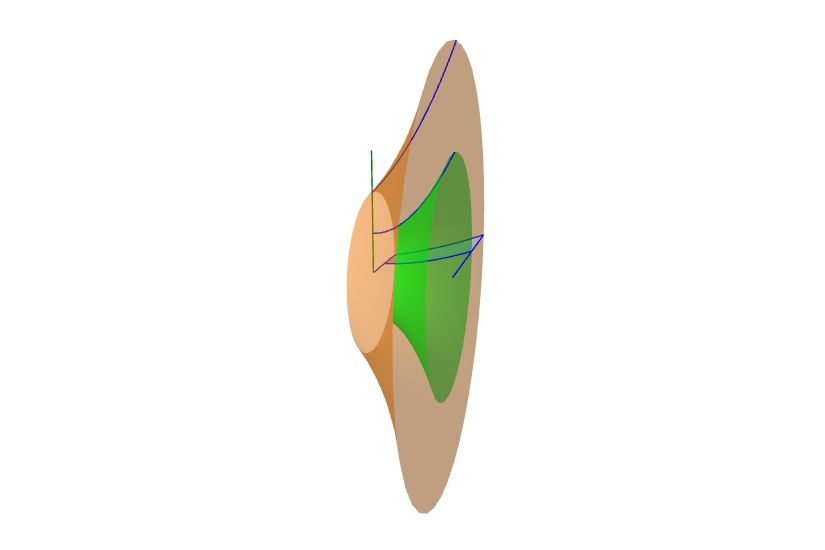
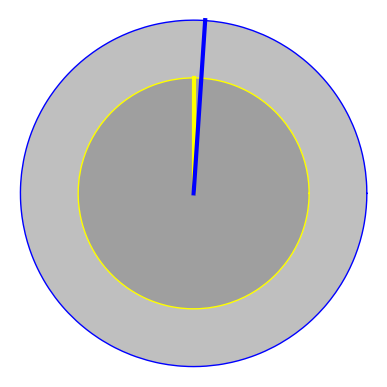
ให้ $f,g $ เป็นฟังก์ชันที่ต่อเนื่องและ$f(x) \geq g(x) \geq k $ทุก $x$ ในช่วงปิด [ a , b] และ
$R$ เป็นบริเวณที่อยูระหว่าง เส้นโค้ง $y=f(x),y=g(x) $ สำหรับ $a \leq x \leq b $
จะได้ว่า ปริมาตรของรูปทรงสามมิติที่เกิดจากการหมุน บริเวณ $R$ รอบเส้นตรง $y=k $ คือ
$$ V = \int_a^b \pi ( [f(x) -k ]^2 - [g(x)-k]^2 ) dx $$
ในทำนองเดียวกัน สำหรับ $R$ เป็นบริเวณที่อยูระหว่าง เส้นโค้ง $x=f(y),x=g(y) ,f(y) \geq g(y) \geq h $ สำหรับ $c \leq y \leq d $
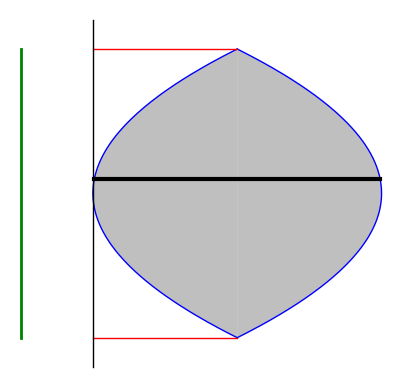
จะได้ว่า ปริมาตรของรูปทรงสามมิติที่เกิดจากการหมุน บริเวณ $R$ รอบเส้นตรง $x=h $ คือ
$$ V = \int_c^d \pi ( [f(y) -h ]^2 - [g(y)-h]^2 ) dy $$
ตัวอย่าง
ให้ $R$ เป็นบริเวณที่ถูกปิดล้อมด้วยเส้นโค้ง $y=\sqrt{x}$ และ $ y = x $
จงหาปริมาตรที่เกิดจากการหมุนบริเวณ $ R $ รอบแกน $x$ และแกน $y$
ตัวอย่าง
ให้ $ R $ เป็นบริเวณที่ถูกปิดล้อมด้วยเส้นโค้ง $x=\sqrt{y} , y = 9 $ และแกน $y$
จงหาปริมาตรที่เกิดจากการหมุนบริเวณ $ R $ รอบเส้นตรง $ x =-2 $ และเส้นตรง $ y = -1$
2. การหาปริมาตรรูปทรงสามมิติโดยวิธีเปลือกทรงกระบอก
จากปริมาตรของรูปทรงเปลือกทรงกระบอกที่มีรัศมีวงนอกคือ $r_2$ และรัศมีวงในคือ $r_1$ ส่วนสูง $h$ได้ว่า
$$V= 2\pi r h \Delta r $$

ให้ $f$ เป็นฟังก์ชันที่ต่อเนื่องและ$f(x) \geq 0 $ทุก $x$ ในช่วงปิด [ a , b] โดยที่ $a \geq 0$ และ
$R$ เป็นบริเวณที่อยู่ใต้เส้นโค้ง $y=f(x)$ แต่อยู่เหนือแกน $x $ สำหรับ $a \leq x \leq b $

จะได้ว่า ปริมาตรของรูปทรงสามมิติที่เกิดจากการหมุน บริเวณ $R$ รอบแกน $y$ คือ
$$ V = \int_a^b 2 \pi x f(x) dx $$
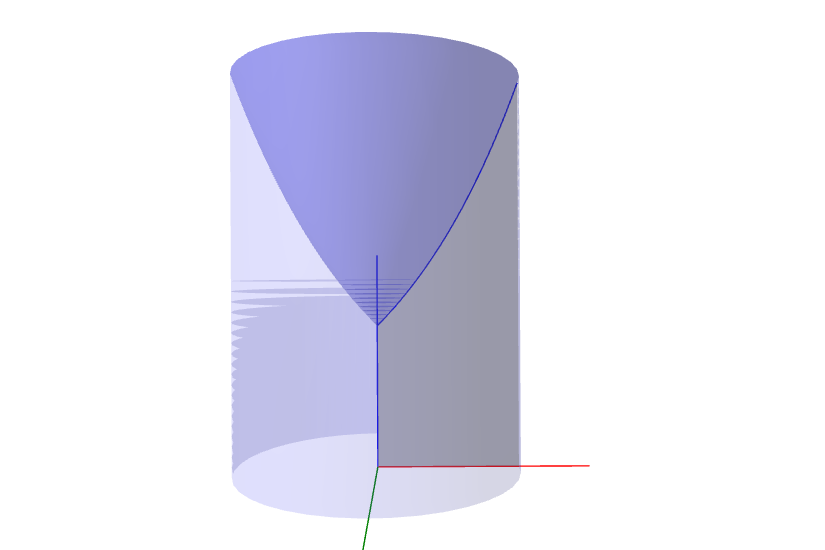
หมายเหตุ
คิดเหมือน $ x $ แทนรัศมี , $f(x) $ แทนความสูง และ $dx$ แทนความหนา
ของเปลือกทรงกระบอก
กรณี
$R$ เป็นบริเวณที่อยู่ระหว่างเส้นโค้ง $y=f(x),y=g(x) ,f(x) \geq g(x) $ ทุก $x $ ที่ $0 \leq a \leq x \leq b $
จะได้ว่า ปริมาตรของรูปทรงสามมิติที่เกิดจากการหมุน บริเวณ $R$ รอบแกน $y$ คือ
$$ V = \int_a^b 2 \pi x (f(x)-g(x)) dx $$
กรณี
$R$ เป็นบริเวณที่อยู่ระหว่างเส้นโค้ง $y=f(x),y=g(x) ,f(x) \geq g(x) $ ทุก $x $ ที่ $ h \leq a \leq x \leq b $
จะได้ว่า ปริมาตรของรูปทรงสามมิติที่เกิดจากการหมุน บริเวณ $R$ รอบแกน $x=h$ คือ
$$ V = \int_a^b 2 \pi (x-h) (f(x)-g(x)) dx $$
ในทำนองเดียวกัน
กรณี
$R$ เป็นบริเวณที่อยู่ระหว่างเส้นโค้ง $x=f(y),x=g(y) ,f(y) \geq g(y) $ ทุก $y $ ที่ $ k \leq c \leq y \leq d $
จะได้ว่า ปริมาตรของรูปทรงสามมิติที่เกิดจากการหมุน บริเวณ $R$ รอบแกน $y=k$ คือ
$$ V = \int_c^d 2 \pi (y-k) (f(y)-g(y)) dy $$
แบบฝึกหัด
จงหาปริมาตรรูปทรงสามมิติที่เกิดจากการหมุนบริเวณที่ปิดล้อมด้วยเส้นโค้ง รอบเส้นตรงที่กำหนดให้
$
\begin{align}
& 1. y=1+x^3,x=1,x=2,y=0 \quad รอบแกน x \\
& 2. y=x^2-x,y=2x-x^2 \quad รอบเส้นตรง y = 2 \\
& 3. x=\sqrt{9-y^2} ,x = 0 ,y=1,y=3 \quad รอบแกน y \\
& 4. y=x,y=\sqrt{x} \quad รอบเส้นตรง y = 1 \\
& 5. x=y^3 ,x=\frac{1}{y} ,x=1,x=2 \quad รอบแกน x \\
& 6. y=4x-x^2,y=3 \quad รอบเส้นตรง x = 1 \\
& 7. y=x^4 , y=\sin (\frac{\pi x}{2}) \quad รอบเส้นตรง x = -1 \\
& 8. x=0 , x=9-y^2 \quad รอบเส้นตรง x = -1 \\
& 9. x=1-y^4 , x=0 \quad รอบเส้นตรง x = 2 \\
\end{align}
$











