กฎลูกโซ่
จากกฎลูกโซ่สำหรับฟังก์ชัน ตัวแปรเดียว ได้ว่า
ถ้า $y=y(u) ,\quad u = u(x) $ แล้วจะได้ว่า $\frac{dy}{dx} \quad = \frac{dy}{du} \cdot \frac{du}{dx}$
สำหรับฟังก์ชันหลายตัวแปร เราจะได้ว่า
ทฤษฎีบท
ถ้า $z=z(x,y) $ เป็นฟังก์ชันที่หาอนุพันธ์ได้ ที่ $x $ และ $y$
และ $x=x(t) ,\quad y=y(t) $ ทั้งสองฟังก์ชันเป็นฟังก์ชันที่หาอนุพันธ์ได้ ที่ $t$ แล้วจะได้ว่า
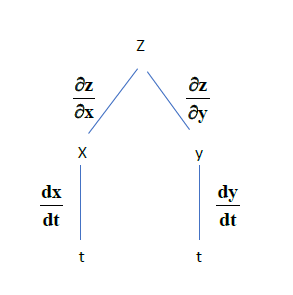
$$ \frac{dz}{dt} \quad = \frac{\partial z}{\partial x} \cdot \frac{dx}{dt} +\frac{\partial z}{\partial y} \cdot \frac{dy}{dt} $$
สามารถเขียนเป็นแผนภาพต้นไม้ได้ดังนี้
ตัวอย่าง
ให้ $z=z(x,y) = x^4 + 3x^2 y^3 + y^5 , x=x(t)=\sin 2t , y=y(t) = \cos 3t $ จงหา $\frac{dz}{dt } $
วิธีทำ
$$ \begin{align}
\frac{dz}{dt } & =\frac{\partial z}{\partial x} \frac{dx}{dt } + \frac{\partial z}{\partial y} \frac{dy}{dt }\\
& = (4x^3+6xy^3 )(2 \cos 2t) + (9x^2y^2 +5y^4) (-3 \sin 3t)
\end{align} $$
ทฤษฎีบท
ถ้า $z=z(x,y) $ เป็นฟังก์ชันที่หาอนุพันธ์ได้ ที่ $x $ และ $y$
และ $x=x(t,s) , \quad y=y(t,s) $ ทั้งสองฟังก์ชันเป็นฟังก์ชันที่หาอนุพันธ์ได้ ที่ $t$ และ $s $ แล้วจะได้ว่า
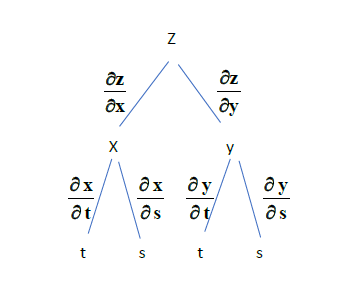
$$ \frac{\partial z}{\partial t} \quad = \frac{\partial z}{\partial x} \cdot \frac{\partial x}{\partial t} +\frac{\partial z}{\partial y} \cdot \frac{\partial y}{\partial t} $$
และ
$$ \frac{\partial z}{\partial s} \quad = \frac{\partial z}{\partial x} \cdot \frac{\partial x}{\partial s} +\frac{\partial z}{\partial y} \cdot \frac{\partial y}{\partial s} $$
สามารถเขียนเป็นแผนภาพต้นไม้ได้ดังนี้
ตัวอย่าง
ให้ $z=z(x,y) = x^3 + y^2 , x=x(t,s)=e^s \sin t , y=y(t,s) = e^s \cos t $ จงหา $\frac{\partial z}{\partial t} , \frac{\partial z}{\partial s} $
วิธีทำ
$$ \begin{align}
\frac{\partial z}{\partial t} & =\frac{\partial z}{\partial x} \frac{\partial x}{\partial t} + \frac{\partial z}{\partial y} \frac{\partial y}{\partial t}\\
& = (3x^2)(e^s \cos t) + (2y) (- e^s \sin t) \\
\frac{\partial z}{\partial s} & =\frac{\partial z}{\partial x} \frac{\partial x}{\partial s} + \frac{\partial z}{\partial y} \frac{\partial y}{\partial s}\\
& = (3x^2)(e^s \sin t) + (2y) (e^s \cos t)
\end{align} $$
ตัวอย่าง
ให้ $z=z(x,y) , x=x(r,s)=r^2+s^3 , y=y(r,s) = 4rs $ จงหา $\frac{\partial z}{\partial r} , \frac{\partial ^2 z}{\partial r^2} $
วิธีทำ
$$ \begin{align}
\frac{\partial z}{\partial r} & = \frac{\partial z}{\partial x} \frac{\partial x}{\partial r} +\frac{\partial z}{\partial y} \frac{\partial y}{\partial r} \\
& = \frac{\partial z}{\partial x} (2r) +\frac{\partial z}{\partial y} (4s) \\
& = 2 r z_x + 4 s z_y \\
\frac{\partial^2 z}{\partial r^2} & = 2 ( z_x + r \frac{\partial z_x}{\partial r} ) +4s \frac{\partial z_y}{\partial r}\\
\end{align} $$
แต่
$$ \begin{align}
\frac{\partial z_x}{\partial r} &= \frac{\partial z_x}{\partial x}\frac{\partial x}{\partial r}+\frac{\partial z_x}{\partial y}\frac{\partial y}{\partial r}
&= z_{xx} (2r) +z_{xy}(4s)
\end{align} $$
และ
$$ \begin{align}
\frac{\partial z_y}{\partial r} &= \frac{\partial z_y}{\partial x}\frac{\partial x}{\partial r}+\frac{\partial z_y}{\partial y}\frac{\partial y}{\partial r}
&= z_{yx} (2r) +z_{yy}(4s)
\end{align} $$
แทนค่าได้
$$ \begin{align}
\frac{\partial ^2 z}{\partial r^2} & = 2 ( z_x + r \frac{\partial z_x}{\partial r} ) +4s \frac{\partial z_y}{\partial r} \\
&= 2 ( z_x + r (z_{xx} (2r) +z_{xy}(4s)) ) +4s (z_{yx} (2r) +z_{yy}(4s)) \\
&= 2z_x +4 r^2 z_{xx} +16 r s z_{xy} +16s^2 z_{yy}
\end{align} $$
กรณี ฟังก์ชันที่มีตัวแปรมากกว่า 2
เราสามารถใช้กฎลูกโซ่ กรณี ฟังก์ชันตัวแปรที่มากกว่า 2 ในทำนองเดียวกัน กล่าวคือ
ถ้า $w=w(x,y,z) $ และ $x=x(r,s,t), \quad y=y(r,s,t), \quad z=z(r,s,t) $ แล้ว
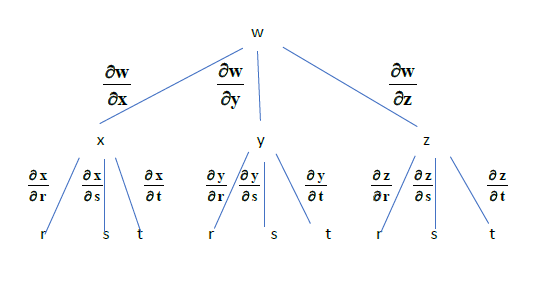
$$ \frac{\partial w}{\partial r} \quad = \frac{\partial w}{\partial x} \cdot \frac{\partial x}{\partial r} +\frac{\partial w}{\partial y} \cdot \frac{\partial y}{\partial r} +\frac{\partial w}{\partial z} \cdot \frac{\partial z}{\partial r} $$
ในการหา $ \frac{\partial w}{\partial s} $ และ $ \frac{\partial w}{\partial t } $ ให้ผู้อ่านลองศึกษาด้วยตนเอง
สามารถเขียนเป็นแผนภาพต้นไ้ม้ได้ดังนี้
อนุพันธ์ของฟังก์ชันแฝง
เราสามารถประยุกต์กฎลูกโซ่ เพื่อใช้หาอนุพันธ์ของฟังก์ชันแฝงได้ ดังนี้
ให้ $y=y(x)$ เป็นฟังก์ชันที่สอดคล้อง สมการ $F(x,y) = 0 $ โดยกฎลูกโซ่เราจะได้ว่า
$$ \frac{\partial F}{\partial x}\frac{dx}{dx}+ \frac{\partial F}{\partial y}\frac{dy}{dx} = 0 $$
ดังนั้น
$$ \frac{dy}{dx} \quad = - \frac{F_x}{F_y}$$
ตัวอย่าง
ให้ $ ัy=y(x) $ เป็นฟังก์ชัน ที่สอดคล้องสมการ $ x^2+3xy +y^4 = \sin x $ จงหา $\frac{dy}{dx} $
วิธีทำ
ให้ $F(x,y) = x^2+3xy +y^4 - \sin x =0 $
ดังนั้น
$$ \begin{align}
\frac{dy}{dx} \quad & = - \frac{F_x}{F_y} \\
& = - \frac{2x+3y- \cos x }{ 3x+4y^3}
\end{align} $$
ให้ $z=z(x,y)$ เป็นฟังก์ชันสองตัวแปรที่สอดคล้อง สมการ $F(x,y,z) = 0 $ โดยกฎลูกโซ่เราจะได้ว่า
$$ \frac{\partial F}{\partial x} \frac{\partial x}{\partial x}+ \frac{\partial F}{\partial z } \frac{\partial z }{\partial x} = 0 $$
ดังนั้น
$$ \frac{\partial z}{\partial x} \quad = - \frac{F_x}{F_z}$$
และ ในทำนองเดียวกัน
$$ \frac{\partial z}{\partial y } \quad = - \frac{F_y}{F_z}$$
ตัวอย่าง
ให้ $z=z(x,y) $ เป็นฟังก์ชันที่สอดคล้องสมการ $ x^3+y^2 + z^3 +4xy^2 z = x+ e^y \sin z $ จงหา $ \frac{\partial z}{\partial x} , \frac{\partial z}{\partial y } $
วิธีทำ
ให้ $ F(x,y,z) = x^3+y^2 + z^3 +4x y^2 z - x- e^y \sin z = 0$
ดังนั้น
$$ \begin{align}
\frac{\partial z}{\partial x} \quad & = - \frac{F_x}{F_z} \\
& = - \frac{3x^2+4y^2 z -1 }{ 3z^2+4xy^2-e^y \cos z } \\
\frac{\partial z}{\partial y} \quad & = - \frac{F_y}{F_z} \\
& = - \frac{2y +8xy z - e^y \sin z }{ 3z^2+4xy^2-e^y \cos z }
\end{align}
$$



