ความหมายเชิงเรขาคณิตของอนุพันธ์
ให้ $y = f(x) $ จะได้ว่า $f'(a)$ คือความชันของเส้นสัมผัสของเส้นโค้ง $ y=f(x)$ ที่จุด $ (a,f(a)) $
ดังนั้น สมการเส้นสัมผัสของเส้นโค้งที่จุด $ (a,f(a)) $ คือ
$$ y-f(a) = f'(a) (x-a) $$
และได้ว่า สมการเส้นตรงที่ตั้งฉากกับเส้นสัมผัสของเส้นโค้งที่จุด $ (a,f(a)) $ คือ
$$ y-f(a) = -\frac{1}{f'(a)} (x-a) $$ เมื่อ $f'(a) \neq 0 $
$$x=a $$เมื่อ $f'(a) = 0 $
ตัวอย่าง
จงหาสมการเส้นสัมผัสของเส้นโค้ง $y = x^2 -x +2$ ที่จุด $(1,2) $
การเขียนกราฟของฟังก์ชัน
บทนิยาม
จะกล่าวว่าฟังก์ชัน $f(x)$ เป็นฟังก์ชันเพิ่มบนเซต $A$ ถ้า ทุก $a,b \in A $ ซึ่ง $a < b$ แล้ว $f(a) < f(b) $
บทนิยาม
จะกล่าวว่าฟังก์ชัน $f(x)$ เป็นฟังก์ชันลดบนเซต $A$ ถ้า ทุก $a,b \in A $ ซึ่ง $a < b$ แล้ว $f(a) > f(b) $
ทฤษฎีบท
ให้ $f(x)$ เป็นฟังก์ชันที่หาอนุพันธ์ได้บนเซต $A$ ดังนั้น
1. ถ้า $f'(x) >0 $ บนเซต $A$ แล้ว $f(x)$ จะเป็นฟังก์ชันเพิ่มบนเซต $ A $
2. ถ้า $f'(x) < 0 $ บนเซต $A$ แล้ว $f(x)$ จะเป็นฟังก์ชันลดบนเซต $ A $
บทนิยาม
ให้ $f(x)$ เป็นฟังก์ชันที่มีความต่อเนื่องบนเซต $A$ ดังนั้น
1. จะกล่าวว่า $f(x) $ มี ค่าสูงสุดสัมบูรณ์ ที่ $ c \in A $ ก็ต่อเมื่อ $f(c) \geq f(x)$ ทุก $x \in A $ เรียกจุด $ (c,f(c)) $ ว่า จุดสูงสุดสัมบูรณ์
2. จะกล่าวว่า $f(x) $ มี ค่าต่ำสุดสัมบูรณ์ ที่ $ c \in A $ ก็ต่อเมื่อ $f(c) \leq f(x)$ ทุก $x \in A$ เรียกจุด $ (c,f(c)) $ ว่า จุดต่ำสุดสัมบูรณ์
3. จะกล่าวว่า $f(x) $ มี ค่าสูงสุดสัมพัทธ์ ที่ $ c \in A $ ก็ต่อเมื่อ มี $\delta > 0 $ ทำให้ $f(c) \geq f(x)$ ทุก $x \in (c-\delta , c+\delta ) $ เรียกจุด $ (c,f(c)) $ ว่า จุดสูงสุดสัมพัทธ์
4. จะกล่าวว่า $f(x) $ มี ค่าต่ำสุดสัมพัทธ์ ที่ $ c \in A $ ก็ต่อเมื่อ มี $\delta > 0 $ ทำให้ $f(c) \leq f(x)$ ทุก $x \in (c-\delta , c+\delta ) $ เรียกจุด $ (c,f(c)) $ ว่า จุดต่ำสุดสัมพัทธ์
5. จะกล่าวว่า $f(x) $ มี ค่าวิกฤติ ที่ $ c \in A $ ก็ต่อเมื่อ มี $ f'(c) = 0 $ หรือ $f'(c)$ หาค่าไม่ได้ เรียกจุด $ (c,f(c)) $ ว่า จุดวิกฤติ
ทฤษฎีบท
ให้ $f(x)$ เป็นฟังก์ชันที่หาอนุพันธ์ได้บนเซต $A$ ดังนั้น
ถ้า $f(x) $ มี ค่าสูงสุดสัมพัทธ์ หรือ ค่าต่ำสุดสัมพัทธ์ ที่ $ c \in A $ แล้ว $f'(c) = 0 $
หมายเหุ
บทกลับของทฤษฎีบท ไม่เป็นความจริง
ตัวอย่าง
$f(x)= x^3$ เห็นได้ว่า $f'(0) = 0 $ แต่ จุด (0,0) ไม่ใช่จุดสูงสุดสัมพัทธ์ และ ไม่ใช่จุดต่ำสุดสัมพัทธ์
ทฤษฎีบท (การทดสอบจุดวิกฤติ)
ให้ $ (c,f(c)) $ เป็นจุดวิกฤติ จะได้ว่า ถ้า มี $\delta > 0 $ ทำให้
1. $f'(x) > 0 $ ทุก $x \in (c-\delta , c) $ และ $f'(x) < 0 $ ทุก $x \in (c, c+\delta ) $
แล้ว $ (c,f(c)) $ จะเป็นจุด สูงสุดสัมพัทธ์
2. $f'(x) < 0 $ ทุก $x \in (c-\delta , c) $ และ $f'(x) > 0 $ ทุก $x \in (c, c+\delta ) $
แล้ว $ (c,f(c)) $ จะเป็นจุด ต่ำ สุดสัมพัทธ์
3. $f'(x) > 0 $ ทุก $x \in (c-\delta , c) $ และ $f'(x) > 0 $ ทุก $x \in (c, c+\delta ) $
แล้ว $ (c,f(c)) $ จะไม่ใช่จุดสูงสุดสัมพัทธ์ และ ไม่ใช่จุดต่ำสุดสัมพัทธ์
4. $f'(x) < 0 $ ทุก $x \in (c-\delta , c) $ และ $f'(x) < 0 $ ทุก $x \in (c, c+\delta ) $
แล้ว $ (c,f(c)) $ จะไม่ใช่จุดสูงสุดสัมพัทธ์ และ ไม่ใช่จุดต่ำสุดสัมพัทธ์
ทฤษฎีบท (การทดสอบจุดวิกฤติ 2)
ให้ $ (c,f(c)) $ เป็นจุดวิกฤติ
1. ถ้า $f''(c) < 0 $ แล้ว $ (c,f(c)) $ จะเป็นจุด สูงสุดสัมพัทธ์
2. ถ้า $ f''(c) > 0 $ แล้ว $ (c,f(c)) $ จะเป็นจุด ต่ำ สุดสัมพัทธ์
3. ถ้า $ f''(c) = 0 $ แล้ว ยังสรุปไม่ได้ เกี่ยวกับจุด $ (c,f(c)) $
บทนิยาม
1. จะกล่าวว่าฟังก์ชัน $f(x)$ จะมีกราฟเว้าบนบนเซต $A$ ถ้า $ f'(x) $ เป็นฟังก์ชันเพิ่มบนเซต $A $
2. จะกล่าวว่าฟังก์ชัน $f(x)$ จะมีกราฟเว้าล่างบนเซต $A$ ถ้า $ f'(x) $ เป็นฟังก์ชันลดบนเซต $A $
3. จะเรียกจุด $(c,f(c) ) $ ว่าจุดเปลี่ยนเว้า ถ้า มี $\delta > 0 $ ทำให้ $f(x)$ มีกราฟที่ความเว้า บนช่วง $(c-\delta , c ) $ ต่างจาก ความเว้าบนช่วง $(c,c+ \delta )$
ทฤษฎีบท
1. ถ้า $f''(x) > 0 $ ทุก $x \in A $แล้ว กราฟของ $ f(x) $ จะมีกราฟเว้าบนบนเซต $A$
2. ถ้า $f''(x) < 0 $ ทุก $x \in A $แล้ว กราฟของ $ f(x) $ จะมีกราฟเว้าล่างบนเซต $A$
หมายเหตุ
ถ้า $ f''(c) = 0 $ แล้ว จุด (c,f(c)) อาจจะเป็นจุดเปลี่ยนเว้า
ตัวอย่าง
$f(x) = x^4 $ จะเห็นได้ว่า $f''(0) = 0 $ แต่ จุด $(0,0) $ ไม่ใช่จุดเปลี่ยนเว้า
$f(x) = -x^4 $ จะเห็นได้ว่า $f''(0) = 0 $ แต่ จุด $(0,0) $ ไม่ใช่จุดเปลี่ยนเว้า
เส้นกำกับแนวดิ่ง และ เส้นกำกับแนวนอน
บทนิยาม
1. เรียกเส้นตรง $ x = c$ ว่า เส้นกำกับแนวดิ่ง ของกราฟของฟังก์ชัน $ y = f(x) $ เมื่อ $\lim_{x \to c^{-} } f(x) = \pm \infty $ หรือ $\lim_{x \to c^{+} } f(x) = \pm \infty $
2. เรียกเส้นตรง $ y = L $ ว่า เส้นกำกับแนวนอน ของกราฟของฟังก์ชัน $ y = f(x) $ เมื่อ $\lim_{x \to \pm \infty } f(x) = L $
ตัวอย่าง
จงหาเส้นกำกับของฟังก์ชันต่อไปนี้
1. $f(x) = \frac{1}{x-1}$
2. $f(x) = \frac{x^2}{x^2-x-6}$
วิธีทำ
1. จาก $ \lim_{x \to 1^{+} } \frac{1}{x-1} = \infty $
ดังนั้น เส้นตรง $x = 1 $ เป็นเส้นกำกับแนวดิ่ง
ข้อสังเกตุ $ \lim_{x \to 1^{-} } \frac{1}{x-1} = - \infty $
และ $ \lim_{x \to \pm \infty} \frac{1}{x-1} = \lim_{x \to \pm \infty } \frac{1}{x} ( \frac{1}{1-\frac{1}{x}} ) = 0 $
ดังนั้น เส้นตรง $y = 0 $ เป็นเส้นกำกับแนวนอน
2. จาก $ \lim_{x \to 3^{+} } \frac{x^2}{x^2-x-6} = \lim_{x \to 3^{+}} (\frac{1}{x-3} )( \frac{x^2}{x+2}) =\infty $
และ $ \lim_{x \to -2^{+}} \frac{x^2}{x^2-x-6} = \lim_{x \to -2^{+}} (\frac{1}{x+2} )( \frac{x^2}{x-3} ) = -\infty $
ดังนั้น เส้นตรง $x = 3 $ และ เส้นตรง $ x=-2 $ เป็นเส้นกำกับแนวดิ่ง
จาก $ \lim_{x \to \pm \infty } \frac{x^2}{x^2-x-6} = \lim_{x \to \pm \infty } \frac{1}{1-\frac{1}{x} -\frac{6}{x^2}} = 1 $
ดังนั้น เส้นตรง $y = 1 $ เป็นเส้นกำกับแนวนอน
ตัวอย่าง
จงพิจารณาอธิบาย ลักษณะ พร้อม วาดกราฟของฟังก์ชันต่อไปนี้
1. $f(x) = \frac{1}{6}(x^3-6x^2+9x+6)$
2. $f(x) = \frac{3-x^2}{1-x^2}$
วิธีทำ
1. ไม่มีค่า $c$ ทำให้ $\lim_{x \to c^{-} } f(x) = \pm \infty $ หรือ $\lim_{x \to c^{+} } f(x) = \pm \infty $
ดังนั้น กราฟของฟังก์ชัน ไม่มีเส้นกำกับแนวดิ่ง
และเนื่องจาก $\lim_{x \to \pm \infty } f(x) = \pm \infty $
ดังนั้น กราฟของฟังก์ชัน ไม่มีเส้นกำกับแนวนอน
หาจุดวิกฤติ
จาก $$f'(x) = \frac{x^2}{2}-2x+\frac{3}{2}$$
และ $f'(x) =0 $ ก็ต่อเมื่อ $ \frac{x^2}{2}-2x+\frac{3}{2} =0 $ หรือ $(x-1)(x-3) = 0 $
ได้ $ x= 1, \quad 3 $
ดังนั้น จุด $(1,f(1)) $ และจุด (3,f(3)) เป็นจุดวิกฤติ
และ $f'(x) > 0 $ ก็ต่อเมื่อ $(x-1)(x-3) > 0 $
ได้ $x < 1 $ หรือ $ x >3 $
นั่นคือ ฟังก์ชัน $f $ เป็นฟังก์ชันเพิ่มเมื่อ $x < 1 $ หรือ $ x >3 $
$f'(x) < 0 $ ก็ต่อเมื่อ $(x-1)(x-3) < 0 $
ได้ $1< x < 3 $
นั่นคือ ฟังก์ชัน $f $ เป็นฟังก์ชันลดเมื่อ $1 < x < 3 $
พิจารณา $$f''(x) = x - 2 $$
ดังนั้น $f''(x) = 0 $ ก็ต่อเมือ $x = 2 $
$f''(x) > 0 $ ก็ต่อเมือ $x > 2 $
$f''(x) < 0 $ ก็ต่อเมือ $x < 2 $
นั่นคือ กราฟ $ f $ มีกราฟเว้าบนเมื่อ $x > 2 $
กราฟ $ f $ มีกราฟเว้าล่างเมื่อ $x < 2 $
และได้ว่า
จุด $(2,f(2)) $ เป็นจุดเปลี่ยนเว้า
และจาก$f''(1) < 0 $ ดังนั้น จุด $(1,f(1) ) $ เป็นจุดสูงสุดสัมพัทธ์
และจาก$f''(3) > 0 $ ดังนั้น จุด $(3,f(3) ) $ เป็นจุดต่ำสุดสัมพัทธ์
หาค่า $f(1) = \frac{5}{3}$
$f(2) = \frac{4}{3}$
$f(3) = 1$
และ $f(0) = 1 $
| ช่วงการพิจารณา |
$f'(x)$ |
$f''(x)$ |
ลักษณะกราฟ |
| $ x < 1 $ |
+ |
- |
กราฟเพิ่ม เว้าล่าง |
| $ 1 < x < 2 $ |
- |
- |
กราฟลดลง เว้าล่าง |
| $2 < x < 3 $ |
- |
+ |
กราฟลดลง เว้าบน |
| $ x > 3 $ |
+ |
+ |
กราฟเพิ่ม เว้าบน |
เขียนกราฟได้ดังนี้
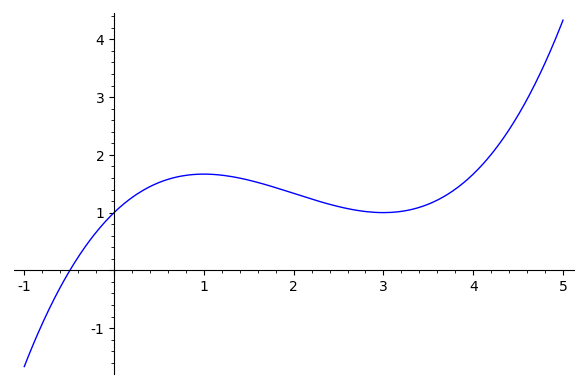
2. ทำเป็นแบบฝึกหัด
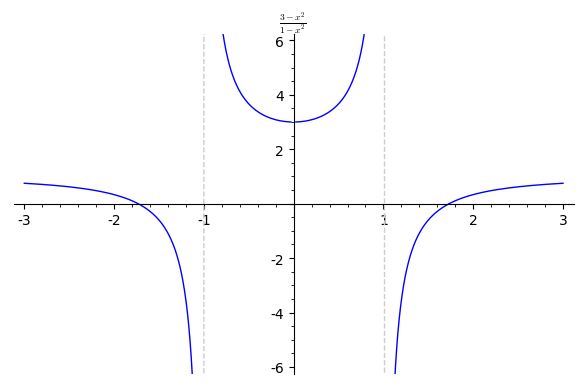
แบบฝึกหัด
จงพิจารณาอธิบาย ลักษณะ พร้อม วาดกราฟของฟังก์ชันต่อไปนี้
$ \begin{align}
&1. f(x) = x^3-9x^2+24x & &
2. f(x) = x^4-2x^2-3 \\
&3. f(x) = 4x^4-32x^3+89x^2-95x+29 & &
4. f(x) = \frac{1}{x^2+2x-2} \\
& 5. f(x) = \frac{x}{x^2-9} & &
6. f(x) = x^2 + \frac{1}{x} \\
\end{align}
$


