อนุพันธ์ของฟังก์ชันประกอบ
ทฤษฎีบท(กฎลูกโซ่)
ให้ $f(x)$ เป็นฟังก์ชันที่หาอนุพันธ์ได้ที่ $x=a$ และ $g(u)$ เป็นฟังก์ชันที่หาอนุพันธ์ได้ที่ $u=f(a)$
ดังนั้น $(gof)(x)$ จะหาอนุพันธ์ได้ที่ $x=a$ และได้ว่า
$$ (gof)'(a) = g'(f(a)) \cdot f'(a)$$
พิสูจน์
สามารเขียนกฎลูกโซ่ ในการหาอนุพันธ์ที่ $x$ ใดๆ ในรูปทั่วไปได้ดังนี้
ถ้า $y=g(u) ,u =f(x) $ แล้ว $$ \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}$$
ตัวอย่าง
ให้ $r(x) =f(g(h(x))) ถ้า h(1) = 2 ,g(2)=3,h'(1)=4,g'(2)=5 ,f'(3)=6 แล้ว จงหาค่า r'(1) $
วิธีทำ
ตัวอย่าง
จงหา $\frac{dy}{dx}$ เมื่อ
$1. y=(3x+5)^9$
$2. y= (\frac{4x^2+5}{x+6})^5 $
วิธีทำ 1
วิธีทำ 2
ทฤษฎีบท(อนุพันธ์ฟังก์ชันผกผัน)
ถ้า $ y=f(x) $ เป็นฟังก์ชันหนึ่งต่อหนึ่ง ที่ $\frac{dy}{dx} \neq 0 $ แล้วจะได้ว่า $$ \frac{dx}{dy} = \frac{1}{\frac{dy}{dx}} $$
สามารถใช้ ทฤษฎีบทอนุพันธ์ฟังก์ชันผกผัน แสดงว่า ถ้า $ y = x^q $ เมื่อ $q $ เป็นจำนวนตรรกยะแล้วจะได้ว่า
$$\frac{dy}{dx} = \frac{d x^q}{dx} = qx^{q-1}$$
ดังนั้นโดยกฎลูกโซ่ได้ว่า ถ้า $y=u^q$ และ $u=u(x)$ แล้ว
$$\frac{dy}{dx} = \frac{d u^q}{dx} = q u^{q-1} \frac{du}{dx}$$
ตัวอย่าง
จงหา $\frac{dy}{dx}$ เมื่อ
$1. y=\sqrt{3x+5} $
$2. y= \frac{4x^2+5}{2+\sqrt{x^2+1}} $
วิธีทำ 1
วิธีทำ 2
อนุพันธ์ฟังก์ชันตรีโกณมิติ
ทฤษฎีบท
ถ้า $u=u(x) $ แล้วจะได้ว่า
$
\begin{align}
& \frac{d}{dx} \sin u = \cos u \frac{du}{dx} &&
\frac{d}{dx} \cos u = - \sin u \frac{du}{dx} \\
& \frac{d}{dx} \tan u = \sec ^2 u \frac{du}{dx}
&& \frac{d}{dx} \cot u = - \csc ^2 u \frac{du}{dx} \\
& \frac{d}{dx} \sec u = \sec u \tan u \frac{du}{dx} & &
\frac{d}{dx} \csc u = - \csc u \cot u \frac{du}{dx} \\
\end{align}
$
พิสูจน์ 1
พิสูจน์ 3
อนุพันธ์ฟังก์ชันตรีโกณมิติผกผัน
จากฟังก์ชัน $\sin x $ ไม่ใช่ฟังก์ชันหนึ่งต่อหนึ่ง บนเซตจำนวนจริง แต่ จะเป็นฟังก์ชัน หนึ่งต่อหนึ่งบนช่วงปิด $[-1,1] $
จะเรียกฟังก์ชันผกผันของฟังก์ชัน $\sin$ ว่า $\arcsin $
ดังนั้น $$ y= \arcsin x \quad ก็ต่อเมื่อ \quad x=\sin y \quad เมื่อ \quad x \in [-1,1] \quad และ \quad y \in [-\frac{\pi}{2},\frac{\pi}{2} ] $$
ในทำนองเดียวกัน จะได้ว่า
$$ y= \arccos x \quad ก็ต่อเมื่อ \quad x=\cos y \quad เมื่อ \quad x \in [-1,1] \quad และ \quad y \in [0,\pi ] $$
$$ y= \arctan x \quad ก็ต่อเมื่อ \quad x=\tan y \quad เมื่อ \quad x \in (-\infty,\infty) \quad และ \quad y \in (-\frac{\pi}{2},\frac{\pi}{2} ) $$
$$ y= arccot x \quad ก็ต่อเมื่อ \quad x=\cot y \quad เมื่อ \quad x \in (-\infty,\infty) \quad และ \quad y \in (0,\pi ) $$
$$ y= arcsec x \quad ก็ต่อเมื่อ \quad x=\sec y \quad เมื่อ \quad x \in (-\infty,-1) \cup (1,\infty) \quad และ \quad y \in [0,\pi] - \{ \frac{\pi}{2} \} $$
$$ y= arccsc x \quad ก็ต่อเมื่อ \quad x=\csc y \quad เมื่อ \quad x \in (-\infty,-1) \cup (1,\infty) \quad และ \quad y \in [-\frac{\pi}{2},\frac{\pi}{2} ] -\{ 0 \} $$
ทฤษฎีบท
ถ้า $u=u(x) $ แล้วจะได้ว่า
$
\begin{align}
& \frac{d}{dx} \arcsin u = \frac{1}{\sqrt{1-u^2}} \frac{du}{dx} &&
\frac{d}{dx} \arccos u = - \frac{1}{\sqrt{1-u^2}} \frac{du}{dx} \\
& \frac{d}{dx} \arctan u =\frac{1}{1+u^2} \frac{du}{dx}
&& \frac{d}{dx} arccot u = - \frac{1}{1+u^2} \frac{du}{dx} \\
& \frac{d}{dx} arcsec u = \frac{1}{|u|\sqrt{u^2-1}} \frac{du}{dx} & &
\frac{d}{dx} arccsc u = - \frac{1}{|u|\sqrt{u^2-1}} \frac{du}{dx} \\
\end{align}
$
พิสูจน์ diff arcsin
พิสูจน์ diff arcsec
ตัวอย่าง
จงหา $\frac{dy}{dx}$ เมื่อ
$1. y = \arcsin (x^2+3) $
$2. y= \arccos (\frac{4x+5}{2+\sin x} ) $
$3. y= x \arctan ( 1+x^2) - arccot (1-x) $
$4. y= x^2 arcsec (x+1) + arccsc (2x+3) $
วิธีทำ1
วิธีทำ2
วิธีทำ3
วิธีทำ4
อนุพันธ์ฟังก์ชันลอการิทึมและฟังก์ชันชี้กำลัง
จาก $\lim_{h \to 0} (1+h)^{\frac{1}{h} } = e \approx 2.71828 $
ได้ว่า
เมื่อ $ x > 0 $ จะได้ว่า
$$ \frac{d}{dx} \log _a x = \frac{1}{x \ln a }$$ เมื่อ $\ln a = \log_e a $
โดยกฎลูกโซ่ทำให้ได้ว่า สำหรับ $ x \in (-\infty,\infty) - \{ 0 \} $ จะได้ว่า
$$ \frac{d}{dx} \log _a | x | = \frac{1}{x \ln a }$$ เมื่อ $\ln a = \log_e a $
และจาก $$ y = a^x \quad ก็ต่อเมื่อ x = \log _a y \quad เมื่อ a \in (0,\infty)- \{ 1 \} , x \in (-\infty,\infty) - \{ 0 \} , y > 0 $$
จะได้ว่า
$$ \frac{d}{dx} a^ x = a^x \ln a $$
ดังนั้น ถ้า $u=u(x) $ แล้วจะได้ว่า
$$ \frac{d}{dx} a^ u = a^u \ln a \frac{du}{dx}$$
กรณี $a= e $ จะได้ว่า
$$ \frac{d}{dx} e^ u = e^u \frac{du}{dx}$$ และ
$$ \frac{d}{dx} \ln | u | = \frac{1}{u} \frac{du}{dx}$$
ตัวอย่าง
จงหา $\frac{dy}{dx}$ เมื่อ
$1. y= 5^x +\frac{1}{2^x} - 5 x e^x $
$2. y= \frac{4x^2+5}{2+e^{4x}} $
$3. y= \log_2 | x^2+3x-4 | $
$4. y= \frac{\ln| x+2| }{2+x+e^{4x}} $
วิธีทำ1
วิธีทำ2
วิธีทำ3
วิธีทำ4
การหาอนุพันธ์ฟังก์ชันโดยใช้ลอการิทึม
ตัวอย่าง
จงหา $\frac{dy}{dx}$ เมื่อ
$1. y= (x^2+3)^x $
$2. y= (5+sin(x))^{(3x^2+1)} $
$3. y= (x^3+x^2+1)^4 (4x+5)^6 \sin (x^2+3) $
$4. y= \frac{(2x+3)(4x-5) }{(1+x^2)(1+e^x)} $
วิธีทำ1
วิธีทำ2
วิธีทำ3
วิธีทำ4
อนุพันธ์ฟังก์ชันไฮเพอร์โบลิก
นิยาม
ฟังก์ชันไฮเพอร์โบลิกไซน์ เขียนแทนด้วย $\sinh $ กำหนดโดย
$$\sinh x = \frac{e^x - e^{-x}}{2}$$
จะได้ว่า
$
\begin{align}
\sinh 0 &= 0 \\
\sinh (-x) &= - \sinh x \\
\lim_{x \to \infty} \sinh x & = \infty \\
\lim_{x \to - \infty} \sinh x & = -\infty \\
\sinh x & < \frac{e^x}{2} \quad ทุก \quad x \\
\end{align}
$
นิยาม
ฟังก์ชันไฮเพอร์โบลิกโคไซน์ เขียนแทนด้วย $ \cosh $ กำหนดโดย
$$\cosh x = \frac{e^x + e^{-x}}{2}$$
จะได้ว่า
$
\begin{align}
\cosh 0 &= 1 \\
\cosh (-x) &= \cosh x \\
\lim_{x \to \infty} \cosh x & = \infty \\
\lim_{x \to - \infty} \cosh x & = \infty \\
\cosh x & > \frac{e^x}{2} \quad ทุก \quad x \\
\end{align}
$
กราฟของ $ \cosh x , \frac{e^x}{2} ,\sinh x$
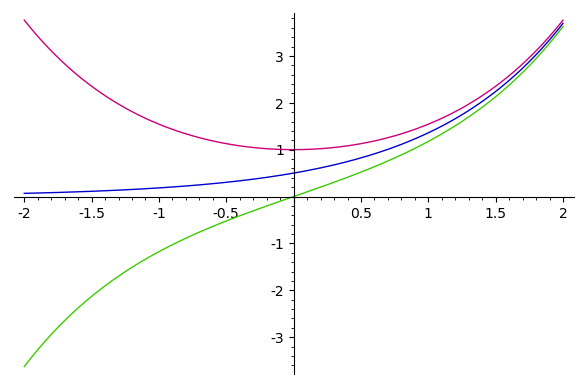
ให้ $t $เป็นจำนวนจริงใดๆ และ $x= \cosh t , y =\sinh t $ จะได้ว่า $x^2-y^2=1$
หรือ $\cosh ^2 t -\sinh ^2 t =1$
นอกจากนี้ยังสามารถพิสูจน์เอกลักษณ์อย่างอื่นได้ดังต่อไปนี้
สำหรับจำนวนจริง $A, B$ ใด ๆ จะได้ว่า
$
\begin{align}
\sinh (A+B) &= \sinh A \cosh B +\cosh A \sinh B \\
\sinh (A-B) &= \sinh A \cosh B - \cosh A \sinh B \\
\cosh (A+B) &= \cosh A \cosh B +\sinh A \sinh B \\
\cosh (A-B) &= \cosh A \cosh B - \sinh A \sinh B \\
\end{align}
$
จากนิยามของ $\sinh x , \cosh x $ สามารถนิยามฟังก์ชัน
ไฮเพอร์โบลิกแทนเจนต์ เขียนแทนด้วย $\tanh $ กำหนดโดย
$$\tanh x = \frac{\sinh x}{\cosh x} $$
ไฮเพอร์โบลิกโคแทนเจนต์ เขียนแทนด้วย $\coth $ กำหนดโดย
$$\coth x = \frac{\cosh x}{\sinh x} $$
ไฮเพอร์โบลิกเซเคนต์ เขียนแทนด้วย $sech $ กำหนดโดย
$$ sech x = \frac{1}{\cosh x} $$
ไฮเพอร์โบลิกโคเซเคนต์ เขียนแทนด้วย $csch $ กำหนดโดย
$$ csch x = \frac{1}{\sinh x} $$
จาก $\frac{d}{dx} e^u = e^u \frac{du}{dx}$ ทำให้ได้อนุพันธ์ของฟังก์ชันไฮเพอร์โบลิกดังต่อไปนี้
สำหรับ $u = f(x) $ จะได้ว่า
$
\begin{align}
\frac{d}{dx} \sinh u &= \cosh u \frac{du}{dx} \\
\frac{d}{dx} \cosh u &= \sinh u \frac{du}{dx} \\
\frac{d}{dx} \tanh u &= sech^2 u \frac{du}{dx} \\
\frac{d}{dx} \coth u &= -csch^2 u \frac{du}{dx} \\
\frac{d}{dx} sech u &= -sech u \tanh u \frac{du}{dx} \\
\frac{d}{dx} csch u &= -csch u \coth u \frac{du}{dx} \\
\end{align}
$
อนุพันธ์ฟังก์ชันไฮเพอร์โบลิกผกผัน
จาก $y =\sinh x =\frac{e^x-e^{-x}}{2}$ ซึ่งเป็นฟังก์ชัน หนึ่งต่อหนึ่ง และทำให้ได้ว่า
$ x= \ln (y+\sqrt{y^2+1})$
ดังนั้น ฟังก์ชันไฮเพอร์โบลิกไซน์ผกผัน เขียนแทนด้วย $\arg \sinh $ และได้ว่า
$$\arg \sinh x = \ln (x+\sqrt{x^2+1})$$
เนื่องจากฟังก์ชันไฮเพอร์โบลิกโคไซน์ ไม่ใช่ ฟังก์ชัน หนึ่งต่อหนึ่ง
ดังนั้นเราจะพิจารณาโดเมนสำหรับฟังก์ชันไฮเพอร์โบลิกโคไซน์ เฉพาะ $[0,\infty) $
ทำให้ได้ว่าสำหรับ $y =\cosh x =\frac{e^x+e^{-x}}{2}$ เมื่อ $ x \geq 0$
จะได้ว่า $y \geq 1 $ และ $ x = \ln ( y+ \sqrt{y^2-1})$
ดังนั้น ฟังก์ชันไฮเพอร์โบลิกโคไซน์ผกผัน เขียนแทนด้วย $\arg \cosh $ และได้ว่า
$$\arg \cosh x = \ln (x+\sqrt{x^2-1}) \quad ทุก \quad x \geq 1 $$
สำหรับ ฟังก์ชันไฮเพอร์โบลิกแทนเจนต์ผกผัน ฟังก์ชันไฮเพอร์โบลิกโคแทนเจนต์ผกผัน
ฟังก์ชันไฮเพอร์โบลิกเซเคนต์ผกผัน และ ฟังก์ชันไฮเพอร์โบลิกโคเซเคนต์ผกผัน สามารถสรุปได้ดังต่อไปนี้
$
\begin{align}
\arg \tanh x &= \frac{1}{2} \ln ( \frac{1+x}{1-x} ) \quad ทุก \quad | x | < 1 \\
\arg \coth x &= \frac{1}{2} \ln ( \frac{x+1}{x-1} ) \quad ทุก \quad | x | > 1 \\
\arg sech x &= \ln ( \frac{1+\sqrt{1-x^2}}{x} ) \quad ทุก \quad 0 < x \leq 1 \\
\arg csch x & = \ln (\frac{1}{x} +\sqrt{1+ \frac{1}{x^2} }) \quad ทุก \quad x \neq 0 \\
\end{align}
$
จาก $\frac{d}{dx} \ln u = \frac{1}{u} \frac{du}{dx}$ ทำให้ได้อนุพันธ์ของฟังก์ชันไฮเพอร์โบลิกผกผันดังต่อไปนี้
สำหรับ $u = f(x) $ จะได้ว่า
$
\begin{align}
\frac{d}{dx} \arg \sinh u &= \frac{1}{\sqrt{u^2+1}} \frac{du}{dx} \\
\frac{d}{dx} \arg \cosh u &= \frac{1}{\sqrt{u^2-1}} \frac{du}{dx} \\
\frac{d}{dx} \arg \tanh u &= \frac{1}{1-u^2} \frac{du}{dx} \\
\frac{d}{dx} \arg \coth u &= \frac{1}{1-u^2} \frac{du}{dx} \\
\frac{d}{dx} \arg sech u &= \frac{-1}{u\sqrt{1-u^2}} \frac{du}{dx} \\
\frac{d}{dx} \arg csch u &= \frac{-1}{|u| \sqrt{1+u^2}} \frac{du}{dx} \\
\end{align}
$
แบบฝึกหัด
จงหา $\frac{dy}{dx}$ เมื่อ
$ \begin{align}
&1. y=(4x+7)^8 + (x^2+3x+4)^5 & &
2. y= (2x+3)^4 + \frac{x+2}{x^2+9} \\
& 3. y= \frac{\sqrt{4x^2+5}}{3+\sqrt{x^2+2}} & &
4. y= \sqrt[5]{2x^7+6} + \frac{4}{\sqrt{x}} \\
&5. y = x \sin (2x^3+x+1) + \cos x^2 & &
6. y = 2x+\tan ^2 (3x+4) - \cot (4x+5) \\
& 7. y = (2x-1) \sec x - \csc (1+x^2) & &
8. y = e^x \sin (1+x^2) +\ln x \\
& 9. y = \frac{x}{1+\ln x} -\log_2 (3x+1) & &
10. y = (x^2+2x+3)^{(1+x^2)} + x^x \\
&11. y = x \arcsin (1+x) & &
12. y = \frac{1}{\arctan x } + \sin e^x \\
& 13. y = arcsec x^2 - x^3 & &
14. y = arccot (x-1) - arccsc (x^2-1) \\
&15. y = (7x^3+8)^5 \sin x \cos ^2 (4-x) & &
16. y = \frac{x^2 \sqrt {x^3+2}}{(x^3+2)^4 (1-x)^2 }
\end{align}
$
วิธีทำ 10
