การหาปริพันธ์ตรรกยะตรีโกณ
ปริพันธ์ที่ อยู่ในรูปแบบ $R(sinx,cosx) dx $
สามารเปลี่ยนเป็นฟังก์ชันตรรกยะโดยแทนค่าด้วยมุมครึ่งดังต่อไปนี้
$ ให้ u =\tan(\frac{x}{2}) , -\frac{\pi}{2} < \frac{x}{2} < \frac{\pi}{2} $
จะได้ว่า
$ x = 2 \arctan u $
$ดังนั้น dx = \frac{2}{1+u^2} du$
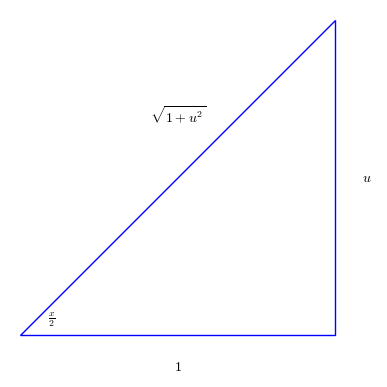
$และ \sin x = 2 \sin \frac{x}{2} \cos \frac{x}{2} = 2 \frac{u}{\sqrt{1+u^2}} \frac{1}{\sqrt{1+u^2}} = \frac{2u}{1+u^2}$
$ \cos x = \cos^2 \frac{x}{2} - \sin^2 \frac{x}{2} = ( \frac{1}{\sqrt{1+u^2}} )^2- (\frac{u}{\sqrt{1+u^2}})^2 = \frac{1-u^2}{1+u^2}$
ตัวอย่าง
จงหาค่าปริพันธ์ $ \int \frac{dx}{1-\sin x +\cos x}$
วิธีทำ
ให้ $ u =\tan(\frac{x}{2}) $
จะได้
$ dx = \frac{2}{1+u^2} du , \sin x =\frac{2u}{1+u^2} , \cos x = \frac{1-u^2}{1+u^2} $
ดังนั้น
$ \int \frac{dx}{1-\sin x +\cos x} = \int \frac{\frac{2 du}{1+u^2}}{1-\frac{2u}{1+u^2} +\frac{1-u^2}{1+u^2}} $
$ = \int \frac{2du}{(1+u^2)-2u+(1-u^2) } $
$= \int \frac{du}{1-u} = - \ln |1-u| +C = - \ln |1-\tan \frac{x}{2} | +C $
แบบฝึกหัด
$
\begin{align}
& 1. \int \frac{dx}{2+\sin x} && 2. \int \frac{dx}{4\sin x - 3 \cos x} \\
& 3. \int \frac{dx}{1+\sin x + \cos x } && 4. \int \frac{dx}{1-\cos x} \\
\end{align}
$
