การหาปริพันธ์โดยการแปลงเป็นฟังก์ชันตรีโกณมิติ
ปริพันธ์ที่ อยู่ในรูปแบบ $\sqrt{a^2-x^2} $ หรือ $\sqrt{x^2-a^2} $ หรือ $\sqrt{a^2+x^2} $ หรือ
รูปแบบทั่วไปคือ $\sqrt{a x^2+bx+c } $ จะใช้เทคนิค การเปลี่ยนตัวแปร โดยเปลี่ยนเป็น ฟังก์ชันตรีโกณมิติดังต่อไปนี้
$
\begin{align}
\sqrt{a^2-x^2} &&ให้ \quad x= a \sin \theta &&จะได้ \quad dx=a\cos \theta d \theta ,\quad \sqrt{a^2-x^2} = a \cos \theta \\
\sqrt{x^2-a^2} &&ให้ \quad x= a \sec \theta &&จะได้ \quad dx = a \sec \theta \tan \theta d \theta ,\quad\sqrt{x^2-a^2} = a \tan \theta \\
\sqrt{a^2+x^2} && ให้ \quad x= a \tan \theta && จะได้ \quad dx=a \sec ^2 \theta d \theta , \quad \sqrt{a^2+x^2} = a \sec \theta \\
\end{align}
$
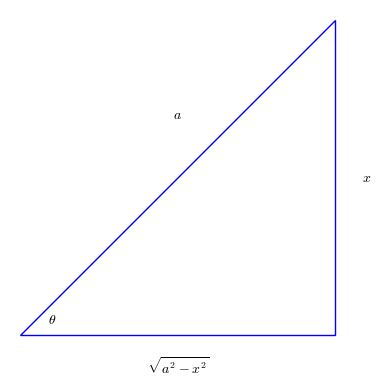
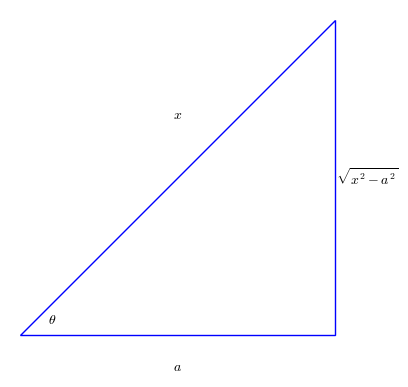
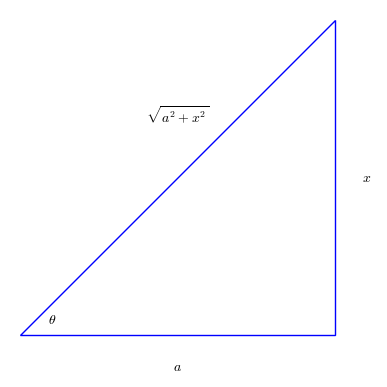
กรณีทั่วไป $\sqrt{a x^2+bx+c } $ จะใช้เทคนิค การทำเป็นกำลังสองสมบูรณ์ จัดรูปเพื่อดูว่าจะอยู่ในรูปแบบใดตามขั้นต้นแล้วค่อยเปลี่ยนเป็นฟังก์ชันตรีโกณมิติ ดังตัวอย่างต่อไปนี้
ตัวอย่าง
$
\begin{align}
& 1. \int \sqrt{4-x^2} dx && 2. \int \frac{\sqrt{x^2-1} }{x} dx \\
& 3. \int x^3 \sqrt{9+x^2} dx && 4. \int \sqrt{x^2+2x+2} dx\\
& 5. \int \frac{x+2}{\sqrt{x^2+2x-3}} dx && 6. \int \sqrt{5-x^2+4x} dx \\
\end{align}
$
วิธีทำ1
วิธีทำ4
แบบฝึกหัด
$
\begin{align}
& 1. \int \sqrt{9-x^2} dx && 2. \int \frac{\sqrt{x^2-25} }{x}dx \\
& 3. \int x^2 \sqrt{4+x^2} dx && 4. \int \sqrt{x^2+4x+5} dx\\
& 5. \int \frac{x+3}{\sqrt{x^2+4x-5}} dx && 6. \int \sqrt{7-x^2+6x} dx \\
\end{align}
$


